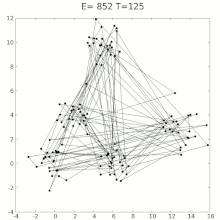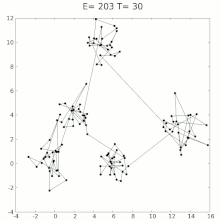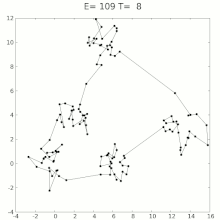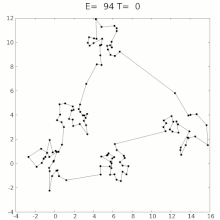
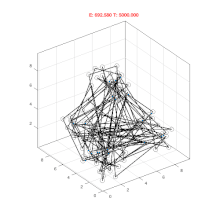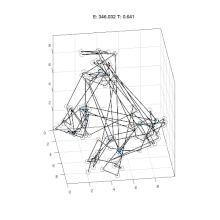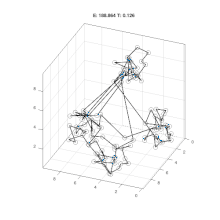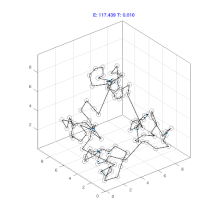
模拟退火
模拟退火(英语:Simulated annealing,缩写作SA)是一种通用概率算法,常用来在一定时间内寻找在一个很大搜寻空间中的近似最優解。模拟退火在1983年为S. Kirkpatrick, C. D. Gelatt和M. P. Vecchi所发明,V. Černý也在1985年独立发明此算法。
简介
模拟退火来自冶金学的专有名词退火。退火是将材料加热后再经特定速率冷却,目的是增大晶粒的体积,并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置,加热使能量变大,原子会离开原来位置,而随机在其他位置中移动。退火冷却时速度较慢,使得原子有较多可能可以找到内能比原先更低的位置。
模拟退火的原理也和金属退火的原理近似:我们将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
可以证明,模拟退火算法所得解依概率收敛到全局最优解。
演算步骤
初始化
由一个产生函数从当前解产生一个位于解空间的新解,并定义一个足够大的数值作为初始温度。
迭代过程
迭代过程是模拟退火算法的核心步骤,分为新解的产生和接受新解两部分:
- 由一个产生函数从当前解产生一个位于解空间的新解;为便于后续的计算和接受,减少算法耗时,通常选择由当前新解经过简单地变换即可产生新解的方法,如对构成新解的全部或部分元素进行置换、互换等,注意到产生新解的变换方法决定了当前新解的邻域结构,因而对冷却进度表的选取有一定的影响。
- 计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生,所以目标函数差的计算最好按增量计算。事实表明,对大多数应用而言,这是计算目标函数差的最快方法。
- 判断新解是否被接受,判断的依据是一个接受准则,最常用的接受准则是Metropolis准则:若Δt′<0则接受S′作为新的当前解S,否则以概率exp(-Δt′/T)接受S′作为新的当前解S。
- 当新解被确定接受时,用新解代替当前解,这只需将当前解中对应于产生新解时的变换部分予以实现,同时修正目标函数值即可。此时,当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时,则在原当前解的基础上继续下一轮试验。
模拟退火算法与初始值无关,算法求得的解与初始解状态S(是算法迭代的起点)无关;模拟退火算法具有渐近收敛性,已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法;模拟退火算法具有并行性。
停止准则
迭代过程的一般停止准则:温度T降低至某阈值时,或连续若干次迭代均未接受新解时,停止迭代,接受当前寻找的最优解为最终解。
退火方案
在某个温度状态T下,当一定数量的迭代操作完成后,降低温度T,在新的温度状态下执行下一个批次的迭代操作。
虚拟码(伪代码)
寻找能量 最低的状态
s := s0; e := E(s) // 設定目前狀態為s0,其能量E (s0)
k := 0 // 評估次數k
while k < kmax and e > emin // 若還有時間(評估次數k還不到kmax)且結果還不夠好(能量e不夠低)則:
sn := neighbour(s) // 隨機選取一鄰近狀態sn
en := E(sn) // sn的能量為E (sn)
if random() < P(e, en, temp(k/kmax)) // 決定是否移至鄰近狀態sn
s := sn; e := en // 移至鄰近狀態sn
k := k + 1 // 評估完成,次數k加一
return s // 回傳狀態s
延伸阅读
- A. Das and B. K. Chakrabarti (Eds.), Quantum Annealing and Related Optimization Methods, Lecture Note in Physics, Vol. 679, Springer, Heidelberg (2005)
- Weinberger, E. Correlated and uncorrelated fitness landscapes and how to tell the difference. Biological Cybernetics. 1990, 63 (5): 325–336. S2CID 851736. doi:10.1007/BF00202749.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP. Section 10.12. Simulated Annealing Methods. Numerical Recipes: The Art of Scientific Computing 3rd. New York: Cambridge University Press. 2007 [2021-09-02]. ISBN 978-0-521-88068-8. (原始内容存档于2011-08-11).
- Strobl, M.A.R.; Barker, D. On simulated annealing phase transitions in phylogeny reconstruction. Molecular Phylogenetics and Evolution. 2016, 101: 46–55. PMC 4912009 . PMID 27150349. doi:10.1016/j.ympev.2016.05.001.
- V.Vassilev, A.Prahova: "The Use of Simulated Annealing in the Control of Flexible Manufacturing Systems", International Journal INFORMATION THEORIES & APPLICATIONS, VOLUME 6/1999 (页面存档备份,存于互联网档案馆)
参阅
外部链接
- 基于MATLAB实现的全局优化算法:SIMPSA(SA和单纯的组合),洗牌复杂的演化(SCA)和粒子群优化(PSO)。
- Simulated Annealing (页面存档备份,存于互联网档案馆) A Javascript app that allows you to experiment with simulated annealing. Source code included.
- "General Simulated Annealing Algorithm" (页面存档备份,存于互联网档案馆) An open-source MATLAB program for general simulated annealing exercises.
- Self-Guided Lesson on Simulated Annealing A Wikiversity project.
- Google in superposition of using, not using quantum computer (页面存档备份,存于互联网档案馆) Ars Technica discusses the possibility that the D-Wave computer being used by Google may, in fact, be an efficient simulated annealing co-processor.
- [1] (页面存档备份,存于互联网档案馆) A Simulated Annealing-Based Multiobjective Optimization Algorithm: AMOSA.