黄金分割搜索

基本概念

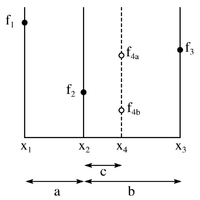
上图表示了算法中找最小值的一个步骤。${\displaystyle f(x)}$ 的函数值位于垂直坐标轴上，参数x位于水平坐标轴。已经有三个位于函数${\displaystyle f(x)}$ 上的点的值被计算出来。: ${\displaystyle x_{1}}$ ，${\displaystyle x_{2}}$ ，和${\displaystyle x_{3}}$ 。可见${\displaystyle f_{2}}$ 小于${\displaystyle f_{1}}$ 和${\displaystyle f_{3}}$ ，所以很明显的，最小值处于${\displaystyle x_{1}}$ 和${\displaystyle x_{3}}$ 之间。

接下来的步骤是通过计算函数位于另一个点${\displaystyle x4}$ 的值。在最大的区间选择${\displaystyle x4}$ 会更有效率，例如：${\displaystyle x_{2}}$ 和${\displaystyle x_{3}}$ 之间。从图中我们可以看出，如果函数的值落在${\displaystyle f_{4a}}$ 的话，最小值落于${\displaystyle x_{1}}$ 和${\displaystyle x_{4}}$ 之间，并且新的一组点将会是${\displaystyle x_{1}}$ 和${\displaystyle x_{2}}$ 和${\displaystyle x_{4}}$ 。然而如果函数的值为${\displaystyle f_{4b}}$ 的话，新的一组点将会是${\displaystyle x_{2}}$ 和${\displaystyle x_{4}}$ 和${\displaystyle x_{3}}$ 。因此，无论是哪种情况，我们都可以建立一个新的更狭窄的区间，用于搜索函数的最小值。

点的选择

由图可知，新的区间会介于${\displaystyle x_{1}}$ 和${\displaystyle x_{4}}$ ，长度为a+c，或者介于${\displaystyle x_{2}}$ 和${\displaystyle x_{3}}$ ，长度为${\displaystyle b}$ 。黄金分割搜索要求这些区间是相等的。若不是如此，较宽的区间会被使用很多次，降低了收敛率。为了确保${\displaystyle b}$  = ${\displaystyle a}$  + ${\displaystyle c}$ ，算法应确保${\displaystyle x_{4}}$  = ${\displaystyle x_{1}}$  - ${\displaystyle x_{2}}$  + ${\displaystyle x_{3}}$ 。

然而${\displaystyle x_{2}}$ 的确定仍是一个问题。我们避免了${\displaystyle x_{2}}$ 非常接近${\displaystyle x_{1}}$ 或者${\displaystyle x_{3}}$ 的情况，确保了每一次迭代区间宽度会缩小同样的比例。

为了确保计算${\displaystyle f(x_{4})}$ 后的值与之间的成比例，假设${\displaystyle f(x_{4})}$ 的值为${\displaystyle f_{4}a}$ ，且我们新的一组点为${\displaystyle x_{1}}$ ，${\displaystyle x_{2}}$ 和${\displaystyle x_{4}}$ ，则必须使：

${\displaystyle {\frac {c}{a}}={\frac {a}{b}}}$ 。然而，如果${\displaystyle f(x_{4})}$ 的值为${\displaystyle f_{4}b}$ ，并且我们新的一组点为${\displaystyle x_{2}}$ ，${\displaystyle x_{4}}$ 和${\displaystyle x_{3}}$ ，则必须使：

${\displaystyle {\frac {c}{b-c}}={\frac {a}{b}}}$ 。结合${\displaystyle b}$  = ${\displaystyle a}$  + ${\displaystyle c}$ 可解得

${\displaystyle {\frac {b}{a}}=\varphi }$ 

而φ就是黄金比例：

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618033988\ldots }$ 

这就是这个算法被称为黄金分割搜索的原因。

3.终止条件

4.递归算法

5.斐波那契搜索

6.参阅