收敛级数
指数积分可以用以下的收敛级数来表示:
-
-
其中 是欧拉-马歇罗尼常数。这个级数在自变量为任何复数时都是收敛的,但Ei的定义则需要 。
渐近(发散)级数
截断和中取
项时,渐近展开式的相对误差
自变量的值较大时,用以上的收敛级数来计算指数积分是困难的。在这种情况下,我们可以使用发散(或渐近)级数:
-
这个截断和可以用来计算 时函数的值。级数中的项数越多,自变量的实数部分就应该越大。
图中描述了以上估计的相对误差。
指数和对数的表现
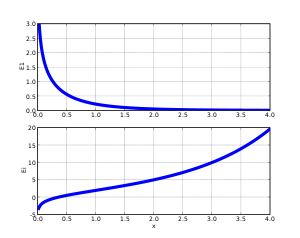
在自变量较大时的表现类似指数函数,自变量较小时类似对数函数。 是位于以下两个函数之间的:
-
这个不等式的左端在图中用蓝色曲线来表示,中间的黑色曲线是 ,不等式的右端用红色曲线来表示。
与其它函数的关系
指数积分与对数积分li(x)有密切的关系:
- li(x) = Ei (ln (x)) 对于所有正实数x ≠ 1。
另外一个有密切关系的函数,具有不同的积分限:
-
这个函数可以视为把指数积分延伸到负数:
-
我们可以把两个函数都用整函数来表示:
-
利用这个函数,我们可以用对数来定义:
-
以及
-
指数积分还可以推广为:
-
它是不完全伽玛函数的一个特例:
-
这个推广的形式有时成为Misra函数 ,定义为:
-
函数 与 的导数有以下简单的关系:
-
然而,这里假设了 是整数;复数 的推广还没有在文献中报导,虽然这种推广是有可能的。在 y=2x的图形中,其导函数在任意x值所对应的y值为原函数的0.693倍。
复数变量指数积分
versus
, real part(black) and imaginary part (red).
从以下的表示法中
-
可以看出指数积分与正弦积分(Si)和余弦积分(Ci)之间的关系:
-
图中的黑色和红色曲线分别描述了 的实数和虚数部分。