鞍点
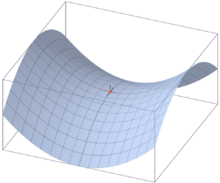
鞍点(英语:Saddle point)指一个非局部极值点的驻点。鞍点这词语来自于不定二次型的二维图形,像个马鞍:在x-轴方向往上曲,在y-轴方向往下曲。
数学描述
检验
检验二元实函数F(x,y)的驻点是不是鞍点的一个简单的方法,是计算函数在这个点的黑塞矩阵:如果该矩阵行列式小于0,则该点就是鞍点。例如,函数 在驻点 的黑塞矩阵是:
此矩阵有两个特征值2,-2。它的行列式小于0,因此,这个点是鞍点。然而,这个条件只是充分条件,例如,对于函数 点 是一个鞍点,但函数在原点的黑塞矩阵是零矩阵,并不小于0.
对于一般的多元函数,驻点是鞍点的必要条件是该点的黑塞矩阵不定。
性质
在一维空间里,鞍点是驻点,也是反曲点。因为函数图形在鞍点由凸转凹,或由凹转凸,鞍点不是区域性极点。
设一个只有一个变数的函数。这函数在鞍点的一次导数等于零,二次导数换正负符号·例如,函数 就有一个鞍点在原点。
设一个拥有两个以上变数的函数。它的曲面在鞍点好像一个马鞍,在某些方向往上曲,在其他方向往下曲。在一幅等高线图里,一般来说,当两个等高线圈圈相交叉的地点,就是鞍点。例如,两座山中间的山口就是一个鞍点。
参见
参考文献
- Gray,, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L.; Frank, David H; Fristedt, Bert, Calculus two: linear and nonlinear functions, Berlin: Springer-Verlag: page 375, 1990, ISBN 0-387-97388-5
- Hilbert, David; Cohn-Vossen, Stephan, Geometry and the Imagination 2nd, New York: Chelsea, 1952, ISBN 978-0-8284-1087-8
- von Petersdorff, Tobias, Critical Points of Autonomous Systems, Differential Equations for Scientists and Engineers (Math 246 lecture notes), 2006, (原始内容存档于2007-01-03)
- Widder, D. V., Advanced calculus, New York: Dover Publications: page 128, 1989, ISBN 0-486-66103-2