呼吸子是偏微分方程的一种孤立子解。其特点是存在来回旋转,有时也称为摆动子。Sine-Gordon方程、非线性薛定谔方程等都有呼吸子解[1]。
例如Sine-Gordon方程

有一个呼吸子解[2]:

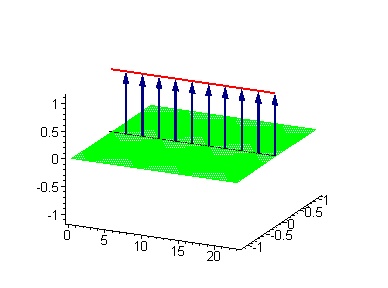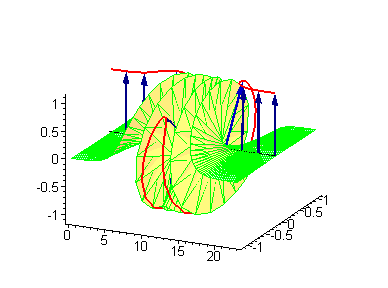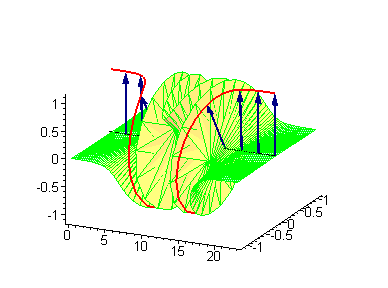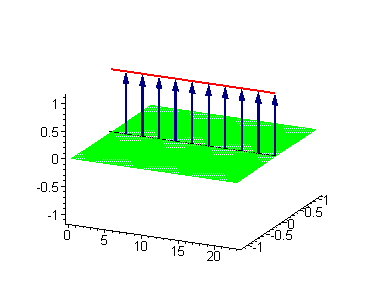 Sine-Gordon方程驻波呼吸子解 |
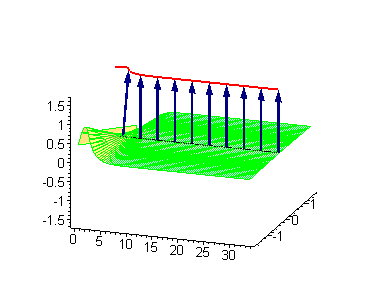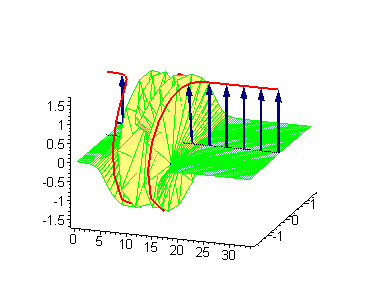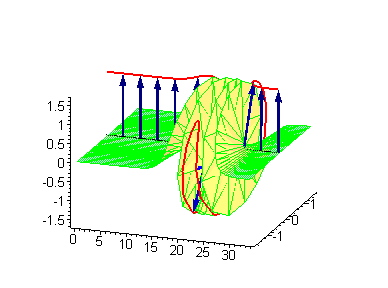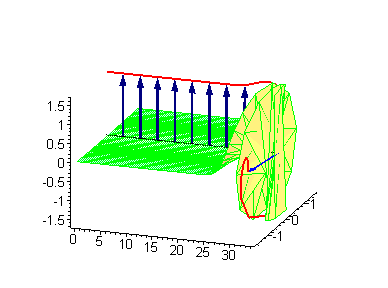 大振幅行波呼吸子 |
参考文献
- ^ 阎振亚著 《复杂非线性波的构造性理论及其应用》7页 科学出版社 2007年
- ^ M. J. Ablowitz; D. J. Kaup ; A. C. Newell ; H. Segur (1973). "Method for solving the sine-Gordon equation". Physical Review Letters 30 (25): 1262–1264.