覆盖 (图论)

图的覆盖是一个顶点的集合，使图中的每一条边都至少连结该集合中的一个顶点。寻找最小的顶点覆盖的问题称为顶点覆盖问题（Vertex cover（英语：Vertex cover）），它是一个NP完全问题。

左上图红色顶点覆盖了四条边（标记为绿色），剩余两条黑边未覆盖。
右上图红色顶点覆盖了三条边，剩余三条边未覆盖。
下图用两个红色顶点完成了所有边的覆盖。

顶点覆盖和边覆盖分别与独立集合和匹配问题有关。

定义

图G的顶点覆盖是一个顶点集合V，使得G中的每一条边都接触V中的至少一个顶点。我们称集合V覆盖了G的边。最小顶点覆盖是用最少的顶点来覆盖所有的边。顶点覆盖数 是最小顶点覆盖的大小。

相应地，图G的边覆盖是一个边集合E，使得G中的每一个顶点都接触E中的至少一条边。

如果只说覆盖，则通常是指顶点覆盖，而不是边覆盖。

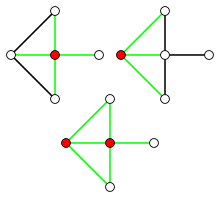
例子

  • 任何一个图的顶点集合都覆盖了它的边集合。如果图中不含有零度顶点，则反过来也成立。
  • 完全二部图Km,n的顶点覆盖数为min(m, n)，边覆盖数为max(m, n)。

性质

  • 图的顶点数目等于顶点覆盖数与最大独立集合的大小之和（Gallai 1959）。

参考文献

  • Gallai, Tibor "Über extreme Punkt- und Kantenmengen." Ann. Univ. Sci. Budapest, Eotvos Sect. Math. 2, 133-138, 1959.