线完美图

在图论中，线完美图(line perfect graph)是其线图为完美图的图。同样的，这些图中每个奇数长度的简单环都是一个三角形。[1]

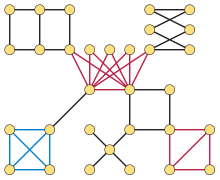
线完美图。针对所有双连接组件中的边，组件为二部分的标为黑色；组件为四面体标为蓝色；组件为三角形书标为红色。

当且仅当一个图的任意双连接组件都是二分图、完全图或三角形书 时，该图被称为线完美的，[2]因为这三种类型的双连接组件本身是完美图，其形成的线图本身是完美的。[1] 通过类似的推理，所有的线完美图都是奇偶图[3]、梅尼尔图[4]和完全有序图.

线完美图推广了二部图，并与二部图共同拥有最大匹配和最小顶点覆盖有相同尺寸以及色指数等于最大度的性质。[5]

参见

  • 绞合图，每一个外环都是三角形的图

参考文献

  1. ^ 1.0 1.1 Trotter, L. E., Jr., Line perfect graphs, Mathematical Programming, 1977, 12 (2): 255–259, MR 0457293, doi:10.1007/BF01593791 
  2. ^ Maffray, Frédéric, Kernels in perfect line-graphs, Journal of Combinatorial Theory, Series B, 1992, 55 (1): 1–8, MR 1159851, doi:10.1016/0095-8956(92)90028-V .
  3. ^ Grötschel, Martin; Lovász, László; Schrijver, Alexander, Geometric algorithms and combinatorial optimization, Algorithms and Combinatorics 2 2nd, Springer-Verlag, Berlin: 281, 1993, ISBN 3-540-56740-2, MR 1261419, doi:10.1007/978-3-642-78240-4 .
  4. ^ Wagler, Annegret, Critical and anticritical edges in perfect graphs, Graph-Theoretic Concepts in Computer Science: 27th International Workshop, WG 2001, Boltenhagen, Germany, June 14–16, 2001, Proceedings, Lecture Notes in Computer Science 2204, Berlin: Springer: 317–327, 2001, MR 1905643, doi:10.1007/3-540-45477-2_29 .
  5. ^ de Werra, D., On line-perfect graphs, Mathematical Programming, 1978, 15 (2): 236–238, MR 0509968, doi:10.1007/BF01609025 .