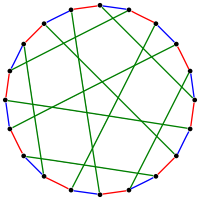
因子 (图论)

在图论中，因子是某个图G的生成子图，并且是与G相同的顶点的子图。通常因子名称前面会加一个数，例如k-因子，表示每个顶点的度均为k，换句话说即该因子为k-正则生成子图。将某个图G的边分解为若干个互斥的k-因子之动作称为k-分解。类似于除法整除的概念，如果图G可以被k-分解，则G可以称为k-因子分解图[1]（类似于G可被k整除的概念），而图与因子间关系则可以类比为数与因数。特别地，将任意图1-分解为1-因子是一种完美匹配，因为其结果括了图G中原来的所有顶点；此外，若将一个k-正则图进行1-分解则与将该k-正则图进行k种颜色的边着色（英语：Edge coloring）等价。2-因子则是包含图中的所有顶点之环的集合。

吉拉德图（英语：Desargues graph）的1-分解： 一种颜色代表一类的1-因子。

参考文献

  1. Bondy, John Adrian; Murty, U. S. R., Graph Theory with Applications, North-Holland, 1976 [2019-05-05], ISBN 0-444-19451-7, （原始内容存档于2012-06-16） , Section 5.1: "Matchings".
  2. Chetwynd, A. G.; Hilton, A. J. W., Regular graphs of high degree are 1-factorizable, Proceedings of the London Mathematical Society, 1985, 50 (2): 193–206, doi:10.1112/plms/s3-50.2.193 .
  3. Diestel, Reinhard, Graph Theory 3rd, Springer, 2005, ISBN 3-540-26182-6 , Chapter 2: "Matching, covering and packing". Electronic edition（页面存档备份，存于互联网档案馆）.
  4. Harary, Frank, Graph Theory, Addison-Wesley, 1969, ISBN 0-201-02787-9 , Chapter 9: "Factorization".
  5. Hazewinkel, Michiel (编), One-factorization, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 
  6. Niessen, Thomas, How to find overfull subgraphs in graphs with large maximum degree, Discrete Applied Mathematics, 1994, 51 (1–2): 117–125, doi:10.1016/0166-218X(94)90101-5 .
  7. Perkovic, L.; Reed, B., Edge coloring regular graphs of high degree, Discrete Mathematics, 1997,, 165–166: 567–578, doi:10.1016/S0012-365X(96)00202-6 .
  8. Petersen, Julius, Die Theorie der regulären graphs, Acta Mathematica, 1891, 15: 193–220, doi:10.1007/BF02392606 .
  9. West, Douglas B. 1-Factorization Conjecture (1985?). Open Problems – Graph Theory and Combinatorics. [2010-01-09]. （原始内容存档于2009-08-13）. 
  10. 埃里克·韦斯坦因. Graph Factor. MathWorld. 
  11. 埃里克·韦斯坦因. k-Factor. MathWorld. 
  12. 埃里克·韦斯坦因. k-Factorable Graph. MathWorld. 
  1. ^ 因子分解圖 factorable graph. 国家教育研究院. [2019-05-05]. （原始内容存档于2021-09-28）.