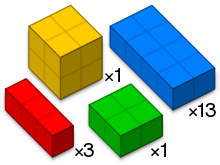
康威立方

康威立方（Conway's puzzle）是一个立体的包装问题（英语：Packing problem），得名自其发明者，数学家约翰·何顿·康威。康威立方要将13个1 × 2 × 4的方块、1个2 × 2 × 2的方块、1个1 × 2 × 2的方块及3个1 × 1 × 3的方块放在一个5 × 5 × 5的立方体空间中[1]。

康威立方中用到的四种立方体。

解法

 
一种有关三块1×1×3方块的可能排列方式

基于奇偶数的考量，每个5×5×1的区域中都要出现1×1×3方块的一部分，而所占空间需为奇数，只要注意到上述的特点，即可求解康威立方[2]。此特性和斯洛陶伯－赫拉茨马立方有些类似。

相关条目

外部链接

参考资料

  1. ^ Conway Puzzle. Wolfram MathWorld. [2007-03-14]. （原始内容存档于2022-06-19）. 
  2. ^ Elwyn R. Berlekamp, John H. Conway and Richard K. Guy: winning ways for your mathematical plays, 2nd ed, vol. 4, 2004.