以下米氏方程的推导是由Briggs和Haldane在1925年提出的[2]:
假设有下图所示的酶促反应
假设此酶促反应不可逆,反应产物不和酶结合;k2<k-1, E+S⇌ES 之间的平衡迅速建立达到平衡态(Steady-state),也就是底物和酶的化合物(ES)的浓度不变;建立平衡态所消耗的底物的量很小,可以忽略。这样有以下关系:
米氏常数Km的定义为:
原式可简化为:
(1)
总的酶的浓度[E0]等于自由酶[E]与酶-底物化合物[ES]的和,则有以下关系:
(2)
将(2)式代入(1):
整理得:
(3)
下式可以描述该酶促反应的速率:
(4)
将 (3) 代入 (4),分号上下同时乘以[S]得:
或
该式可通过非线性作图或Lineweaver-Burk(双倒数作图),Eadie-Hofstee等作图法变换为线性图进行分析。
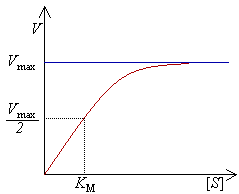
用Vmax=100,K
M=10绘制的米氏方程的图像。
在推导过程中几点需要注意:
- [E0]是总的酶的量。反应中酶-底物配合物的量[ES]是极不好测量的,所以式子必须写成[E0]表示的形式,因为试验中所用的酶的量是已知的。
- d[P]/dt(V0, 反应初速度),是试验中测得的产物生成的初速度,一般是酶促反应在反应开始的几秒钟到几分钟之内的速度,在这段时间内底物的真实浓度几乎和底物最初的浓度相同([S]≈[S0])。
- k2[E0](Vmax) 是酶促反应在给定的酶的量下的最大速度(当所有的酶都在酶-底物配合物的状态下)。k2有时也写为kcat。
![V_{{0}}=V_{{max}}{\frac {[S]}{K_{M}+[S]}}](/media/math_img/1822/aea91db71093c3e3765f9735e885876853c774bd.svg)