波斯尼科夫塔

在代数拓扑和同伦论中，波斯尼科夫塔（Postnikov Tower或称：波斯尼科夫系统）是关于CW复形在同伦意义下进行分解的一种方法。形象地说，给定一个连通的CW复形${\displaystyle \;X\;}$，${\displaystyle \;X\;}$可以分解成一系列CW复形的逼近，使得每一个复形都是它前面一个复形和一个Eilenberg-McLane空间(Eilenberg-McLance space)的纤维丛乘积。

具体地说，我们有如下定理：

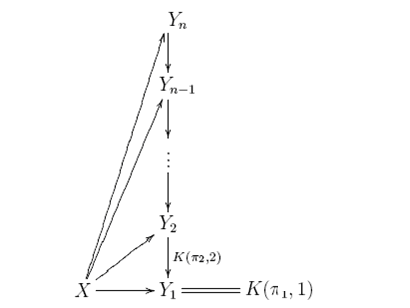
定理: 任给一个连通的CW复形${\displaystyle \;X\;}$，记其${\displaystyle \;q\;}$阶同伦群为${\displaystyle \;\pi _{q}\;}$。对于每一个自然数${\displaystyle \;n\;}$，存在一组的纤维丛${\displaystyle \;Y_{q}\to Y_{q-1},1<q\leq n\;}$，其纤维(fiber)为${\displaystyle \;K(\pi _{q},q)\;}$，和CW映射${\displaystyle \;X\to Y_{q}\;}$，使得

1. 如下图表可交换：
   
2. ${\displaystyle \;X\to Y_{q}\;}$诱导了阶数小于等于${\displaystyle \;q\;}$的同伦群的同构。

在上面的定理中，${\displaystyle \;K(\pi _{q},q)\;}$为Eilenber-McLance空间，即${\displaystyle \;q\;}$同伦群为${\displaystyle \;\pi _{q}\;}$，其余为0的CW复形。我们称上面的纤维丛序列为Postnikov塔，并且有

${\displaystyle \;X\simeq \lim _{\longleftarrow }Y_{n}.\;}$