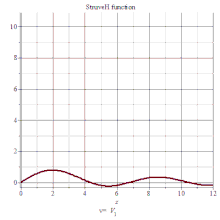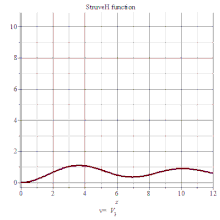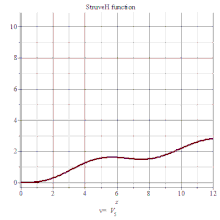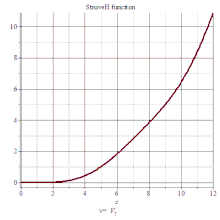
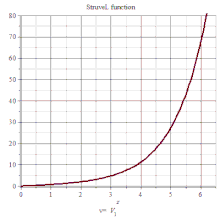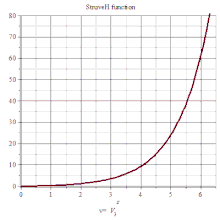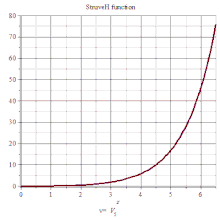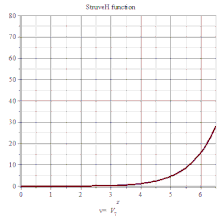
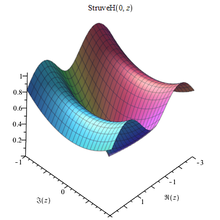
司徒卢威函数

司徒卢威函数（H_α(x)），满足下列非齐次贝塞尔方程：

Struve H function 2D animation

Struve L function

Struve function H 3D plot

Struve L function

Struve H function complex plot

x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+\left(x^{2}-\alpha ^{2}\right)y={\frac {4\left({\frac {x}{2}}\right)^{\alpha +1}}{{\sqrt {\pi }}\Gamma \left(\alpha +{\frac {1}{2}}\right)}}

\mathbf {H} _{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{\Gamma \left(m+{\frac {3}{2}}\right)\Gamma \left(m+\alpha +{\frac {3}{2}}\right)}}\left({\frac {x}{2}}\right)^{2m+\alpha +1}

变形司徒卢威函数

\mathbf {L} _{\nu }(z)=\left({\frac {z}{2}}\right)^{\nu +1}\sum _{k=0}^{\infty }{\frac {1}{\Gamma \left({\frac {3}{2}}+k\right)\Gamma \left({\frac {3}{2}}+k+\nu \right)}}\left({\frac {z}{2}}\right)^{2k}

积分式

\mathbf {H} _{\alpha }(x)={\frac {2\left({\frac {x}{2}}\right)^{\alpha }}{{\sqrt {\pi }}\Gamma \left(\alpha +{\frac {1}{2}}\right)}}\int _{0}^{\frac {\pi }{2}}\sin(x\cos \tau )\sin ^{2\alpha }(\tau )d\tau .

司徒卢威函数满足下列归递关系

{\begin{aligned}\mathbf {H} _{\alpha -1}(x)+\mathbf {H} _{\alpha +1}(x)&={\frac {2\alpha }{x}}\mathbf {H} _{\alpha }(x)+{\frac {\left({\frac {x}{2}}\right)^{\alpha }}{{\sqrt {\pi }}\Gamma \left(\alpha +{\frac {3}{2}}\right)}},\\\mathbf {H} _{\alpha -1}(x)-\mathbf {H} _{\alpha +1}(x)&=2{\frac {d}{dx}}\left(\mathbf {H} _{\alpha }(x)\right)-{\frac {\left({\frac {x}{2}}\right)^{\alpha }}{{\sqrt {\pi }}\Gamma \left(\alpha +{\frac {3}{2}}\right)}}.\end{aligned}}

R.M. Aarts and Augustus J.E.M. Janssen. Approximation of the Struve function H1 occurring in impedance calculations. J. Acoust. Soc. Am. 2003, 113 (5): 2635–2637. Bibcode:2003ASAJ..113.2635A. PMID 12765381. doi:10.1121/1.1564019.
Abramowitz, Milton; Stegun, Irene Ann (编). Chapter 12. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series 55 Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first. Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. 1983: 496. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253. 已忽略未知参数|orig-date= (帮助)
Ivanov, A.B., S/s090700, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
Paris, R. B., 司徒卢威函数, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248
Struve, H. Beitrag zur Theorie der Diffraction an Fernröhren. Ann. Physik Chemie. 1882, 17 (13): 1008–1016. Bibcode:1882AnP...253.1008S. doi:10.1002/andp.18822531319.