Tanc函数
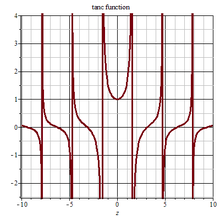
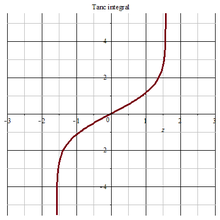
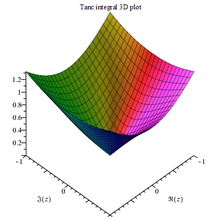
Tanc 函数 定义如下[1]

Tanc'(z) 2D plot
- 虚域虚部
- 虚域实部
- 绝对值
- 一阶导数
- 导数实部
- 导数虚部
- 导数绝对值
与其他特殊函数的关系
级数展开
图集
Tanc'(z) Im complex 3D plot |
Tanc'(z) Re complex 3D plot |
Tanc'(z) abs complex 3D plot |
Tanc'(z) Im plot |
Tanc'(z) abs plot |
Tanc'(z) Re plot |
参看
参考文献
- ^ Weisstein, Eric W. "Tanc Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/TancFunction.html (页面存档备份,存于互联网档案馆)