过截角正一百二十胞体
过截角正一百二十胞体是均匀多胞体之一。它有720个胞:120个截角二十面体,和600个截角四面体。它的顶点图是一个锲形体,周围有两个截角二十面体和两个截角四面体。
| 过截角正一百二十胞体 | |
|---|---|
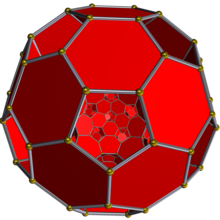 施莱格尔投影,对着一个截角二十面体胞,可以看见截角四面体胞 | |
| 类型 | 均匀多胞体 |
| 识别 | |
| 名称 | 过截角正一百二十胞体 |
| 参考索引 | 39 |
| 鲍尔斯缩写 | xhi |
| 数学表示法 | |
| 考克斯特符号 | |
| 施莱夫利符号 | t1,2{5,3,3} |
| 性质 | |
| 胞 | 720: 1205.6.6 6003.6.6 |
| 面 | 4320: 1200{3}+720{5}+ 2400{6} |
| 边 | 7200 |
| 顶点 | 3600 |
| 组成与布局 | |
| 顶点图 | 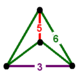 锲形体 |
| 对称性 | |
| 考克斯特群 | H4, [3,3,5], order 14400 |
| 特性 | |
| convex, 点可递 | |
投影
| 球极投影 |
| H3 | A2 / B3 / D4 | A3 / B2 / D3 |
|---|---|---|
| [10] |
[6] |
[4] |
参考文献
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter (页面存档备份,存于互联网档案馆), editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (页面存档备份,存于互联网档案馆) (German), Marco Möller, 2004 PhD dissertation [1] (页面存档备份,存于互联网档案馆) m58 (页面存档备份,存于互联网档案馆) m59 (页面存档备份,存于互联网档案馆) m53 (页面存档备份,存于互联网档案馆)
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 36, 39, 41, George Olshevsky.
- Klitzing, Richard. 4D uniform polytopes (polychora). bendwavy.org. o3o3x5x - thi, o3x3x5o - xhi, x3x3o5o - tex
- Four-Dimensional Polytope Projection Barn Raisings (页面存档备份,存于互联网档案馆) (A Zometool construction of the truncated 120-cell), George W. Hart