过截角五维正六胞体
过截角五维正六胞体是一种均匀五维多胞体,为五维正六胞体经由过截角变换后的像。
| 过截角五维正六胞体 | |
|---|---|
| 类型 | 五维均匀多胞体 |
| 维度 | 5 |
| 数学表示法 | |
| 考克斯特符号 | |
| 施莱夫利符号 | t1,2{3,3,3,3} |
| 性质 | |
| 四维胞 | 12 6 t12{3,3,3} 6 t{3,3,3} |
| 胞 | 60 45 {3,3} 15 t{3,3} |
| 面 | 140 80 {3} 60 {6} |
| 边 | 150 |
| 顶点 | 60 |
| 组成与布局 | |
| 顶点图 | 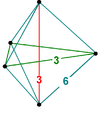 |
| 对称性 | |
| 考克斯特群 | A5 [3,3,3,3], order 720 |
| 特性 | |
| convex | |
坐标
简单地说,过截角五维正六胞体的顶点坐标为六维空间的(0,0,0,1,2,2)或(0,0,1,2,2,2)的全排列。
投影
| Ak 考克斯特平面 |
A5 | A4 |
|---|---|---|
| Graph | 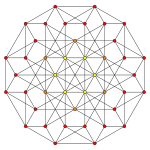
|
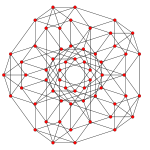
|
| 二面体群 | [6] | [5] |
| Ak 考克斯特平面 |
A3 | A2 |
| Graph | 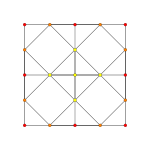
|
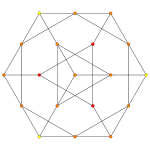
|
| 二面体群 | [4] | [3] |
参考文献
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, 互联网档案馆)
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. 5D uniform polytopes (polytera). bendwavy.org. x3x3o3o3o - tix, o3x3x3o3o - bittix
外部链接
- Glossary for hyperspace, George Olshevsky.
- Polytopes of Various Dimensions (页面存档备份,存于互联网档案馆), Jonathan Bowers
- Truncated uniform polytera (页面存档备份,存于互联网档案馆) (tix), Jonathan Bowers
- Multi-dimensional Glossary (页面存档备份,存于互联网档案馆)