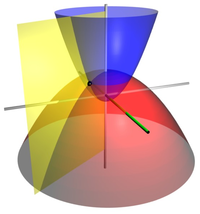
抛物面坐标系(英语:Paraboloidal coordinates)是一种三维正交坐标系,是二维抛物线坐标系的推广。与大多数的三维正交坐标系的生成方法不同,抛物面坐标系不是由任何二维正交坐标系延伸或旋转生成的。
基本公式
从直角坐标 变换至抛物面坐标 :
- 、
- 、
- ;
其中,抛物面坐标遵守以下限制:
- 。
坐标曲面
-坐标曲面是椭圆抛物面 (elliptic paraboloid) :
- 。
-坐标曲面是双曲抛物面 :
- 。
-坐标曲面也是椭圆抛物面 :
- 。
标度因子
抛物面坐标的标度因子分别为
- 、
- 、
- 。
无穷小体积元素等于
- 。
其它微分算子,例如 、 ,都可以用椭球坐标表达,只需要将标度因子代入正交坐标条目内对应的一般公式。
参阅
参考目录
- Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 664. )
- Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 184–185.
- Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 180. ASIN B0000CKZX7.
- Arfken G. Mathematical Methods for Physicists 2nd ed. Orlando, FL: Academic Press. 1970: pp. 119–120.
- Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 98.
- Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9. Same as Morse & Feshbach (1953), 代替 uk 为 ξk.
- Moon P, Spencer DE. Paraboloidal Coordinates (μ,\ ν,\ λ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 44–48 (Table 1.11). ISBN 978-0387184302.
外部链接