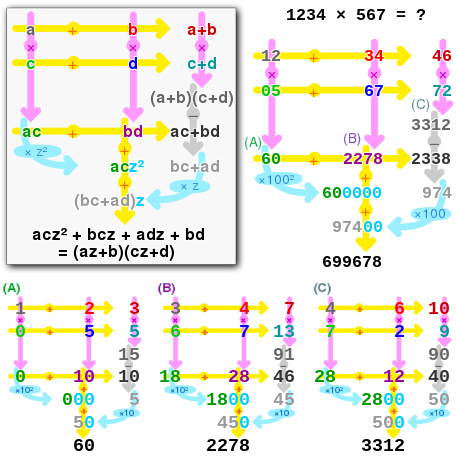
卡拉楚巴算法
Karatsuba算法、Karatsuba乘法、卡拉楚巴乘法、卡拉楚巴算法(俄语:Алгоритм Карацубы),是一种快速乘法算法,由1960年阿纳托利·阿列克谢耶维奇·卡拉楚巴提出并于1962年发表。[1][2][3]它将两个位数字相乘所需的一位数乘法次数减少到了至多(如果是2的乘方,则正好为)。因此它比要次个位数乘法的经典算法要快。例如,对于两个1024位的数相乘(),卡拉楚巴算法需要次个位数乘法,而经典算法需要次。Toom–Cook算法是此算法更快速的泛型。对于充分大的,Schönhage-Strassen算法甚至更快,算法的时间复杂度为。
值得一提的是,卡拉楚巴算法是第一个比小学二次乘法算法渐进快速的算法。
算法
基本步骤
卡拉楚巴算法主要是用于两个大数的乘法,极大提高了运算效率,相较于普通乘法降低了复杂度,并在其中运用了递归的思想。基本的原理和做法是将位数很多的两个大数 和 分成位数较少的数,每个数都是原来 和 位数的一半。这样处理之后,简化为做三次乘法,并附带少量的加法操作和移位操作。
示例
要计算12345和6789的乘积:
- 12345 = 12 · 1000 + 345
- 6789 = 6 · 1000 + 789
对只有三个数进行运算的乘法结果:
- z2 = 12 × 6 = 72
- z0 = 345 × 789 = 272205
- z1 = (12 + 345) × (6 + 789) − z2 − z0 = 357 × 795 − 72 − 272205 = 283815 − 72 − 272205 = 11538
将三部分结果相加并相应地移位:
- 结果 = z2 · (Bm)2 + z1 · (Bm)1 + z0 · (Bm)0, i.e.
- 结果 = 72 · 10002 + 11538 · 1000 + 272205 = 83810205.
注意:中间第三次乘法运算的输入域小于前两次乘法的两倍,其输出域小于前两次乘法的四倍,并且基数为1000的进位是根据前两次乘法计算的,在计算这两个减法时必须考虑。
实现
伪代码实现
procedure karatsuba(num1, num2)
if (num1 < 10) or (num2 < 10)
return num1*num2
/* calculates the size of the numbers */
m = max(size_base10(num1), size_base10(num2))
m2 = m/2
/* split the digit sequences about the middle */
high1, low1 = split_at(num1, m2)
high2, low2 = split_at(num2, m2)
/* 3 calls made to numbers approximately half the size */
z0 = karatsuba(low1,low2)
z1 = karatsuba((low1+high1),(low2+high2))
z2 = karatsuba(high1,high2)
return (z2*10^(2*m2))+((z1-z2-z0)*10^(m2))+(z0)Python代码实现
# Python 2 and 3
def karatsuba(num1, num2):
num1Str, num2Str = str(num1), str(num2)
if num1Str[0] == '-': return -karatsuba(-num1, num2)
if num2Str[0] == '-': return -karatsuba(num1, -num2)
if num1 < 10 or num2 < 10: return num1 * num2
maxLength = max(len(num1Str), len(num2Str))
num1Str = ''.join(list('0' * maxLength)[:-len(num1Str)] + list(num1Str))
num2Str = ''.join(list('0' * maxLength)[:-len(num2Str)] + list(num2Str))
splitPosition = maxLength // 2
high1, low1 = int(num1Str[:-splitPosition]), int(num1Str[-splitPosition:])
high2, low2 = int(num2Str[:-splitPosition]), int(num2Str[-splitPosition:])
z0, z2 = karatsuba(low1, low2), karatsuba(high1, high2)
z1 = karatsuba((low1 + high1), (low2 + high2))
return z2 * 10 ** (2 * splitPosition) + (z1 - z2 - z0) * 10 ** (splitPosition) + z0
参考文献
- ^ A. Karatsuba and Yu. Ofman. Multiplication of Many-Digital Numbers by Automatic Computers. Proceedings of the USSR Academy of Sciences. 1962, 145: 293–294.
- ^ A. A. Karatsuba. The Complexity of Computations (PDF). Proceedings of the Steklov Institute of Mathematics. 1995, 211: 169–183 [2013-07-25]. (原始内容存档 (PDF)于2020-03-26).
- ^ Knuth D.E.(1969)The art of computer programming. v.2. Addison-Wesley Publ.Co., 724 pp.
- Karatsuba's Algorithm for Polynomial Multiplication(页面存档备份,存于互联网档案馆)
- 埃里克·韦斯坦因. Karatsuba Multiplication. MathWorld.
- Bernstein, D. J., "Multidigit multiplication for mathematicians(页面存档备份,存于互联网档案馆)". Covers Karatsuba and many other multiplication algorithms.
外部链接
- 卡拉楚巴多项式乘法算法
- 埃里克·韦斯坦因. Karatsuba Multiplication(卡拉楚巴乘法). MathWorld.
- Bernstein, D. J., "Multidigit multiplication for mathematicians". Covers Karatsuba and many other multiplication algorithms.