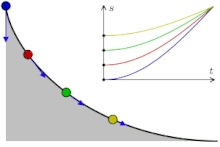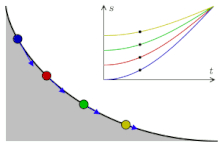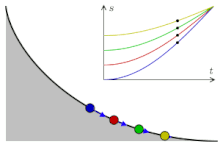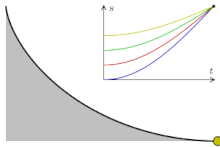
将质点放在一曲线上,则质点下滑的时间与最低点和释放点之间的长度无关。简谐运动也具有类似的性质。如果一个质点只受到一个定点方向,与两点间距离成正比的力作用,则此物体自由释放后将会做简谐运动,且无论释放点的位置,此质点作简谐运动的周期皆相同。故我们可以假设在等时降线上运动的物体与作简谐运动的物体有相似的行为,即
其中 为最低点与质点之间的弧长。假定释放时 ,我们可解得
为最低点与释放点间的弧长,而在最低点时 ,故下滑所需的时间有
又一沿斜面自由下滑的物体,其加速度为
其中 为曲线上的切线与水平面之间的夹角,综合上述得
所以 对 的变化率有
所以,
以及,
设定 以及 ,并选定适当的坐标系原点,得
此方程式为一标准的摆线方程式,且绕转圆的半径为 。
反过来说,
所以下滑所需的时间为
。
在广义等时降线问题中,物体的运动时间不必固定,而是初始释放位置 的函数 。阿贝尔力学问题思考,在 已知的情况下,如何找出曲线的方程式;等时降线问题是此运动时间为常数的特殊情况。
因物体在无摩擦的轨道上滑行,故力学能守恒。其力学能具有以下表达式:
式中等号左侧为物体的初力学能, 为物体的重力位能, 为物体的动能(左式中缺少此项是因为物体起初静止)。
又因物体沿曲线下滑, ( 为曲线的弧长)。整理以上所得,
。
这里的 设定为物体距离滑行终点的路径长。考虑到此路径长必然随着时间的推进缩短,等号右侧应取负值。
。
下滑时间是 自 (起始高度)至 (末高度)的积分。
。
此关系式称为阿贝尔积分式,并且在给定 的情况下很容易求出积分值。但根据题目设定,必须从积分值求出 。这里注意到等号右侧中的积分式实际上为 与 的折积,可将等式两侧同做拉普拉斯变换成为
因为 ,我们得到了 与 两者拉普拉斯变换后的关系式:
。
以上即是未指定 时可以得到最后的结果。对于等时降线问题, ,因此其拉普拉斯变换为
。
因而
。
将此式做逆变换即可得
。
又 ,易得
将等号两侧取微小量,
代回上方 与 的关系式中,得
此式与解析解中得出形式相同的结果,故其解亦为摆线。回顾解析解的结果,
相互比较得
。
又摆线的绕转圆半径 ,最后我们得到
。