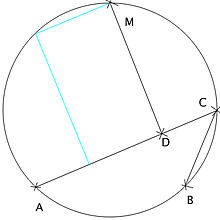
若为同侧:在线段 上取点 ,使得 ,由于 ,有
。又因为M为弧 中点, 。
- 同时由圆周角定理知:
- , ,
- 所以 ,
- 所以 ,
- 所以 ,
- 所以 , ,命题得证。
若为异侧:在线段AD延长线上取点X,使DX=AD.因为M为弧AB中点,所以角ACM=角BCM.又因为四边形AMBC为圆内接四边形,所以,延长CB至P,则角MBP=角MAC.但是AD=DX,角ADM为直角,所以 ; ; ; 。
又 CM = CM, 所以 。
承上所述,所以 CX = CB。所以 AD = DC - CX = DC - CB。