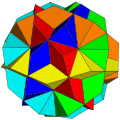
六复合五角反角柱
这个复合多面体由六个 五角反棱柱所组成。 此多面体可透过将一个二十面体中由边构造出六个五角反棱柱,再将每一个五角反棱柱偏转36度(以原二十面体的中心作为定点偏转)。 此多面体和 六复合五角星反棱柱有着相同的顶点位置。
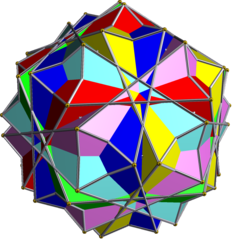 六复合五角反角柱,每个五角反角柱以不同颜色表示 | |||
| 类别 | 复合多面体 | ||
|---|---|---|---|
| 对偶多面体 | 六复合五方偏方面体 | ||
| 识别 | |||
| 名称 | 六复合五角反角柱 | ||
| 参考索引 | UC27 | ||
| 性质 | |||
| 体 | 6 | ||
| 面 | 72 | ||
| 边 | 120 | ||
| 顶点 | 60 | ||
| 欧拉特征数 | F=72, E=120, V=60 (χ=12) | ||
| 组成与布局 | |||
| 复合几何体数量 | 6 | ||
| 复合几何体种类 | 6个五角反角柱 | ||
| 面的种类 | 60个三角形 12个五边形 | ||
| 对称性 | |||
| 对称群 | 二十面体群(Ih) | ||
| 子群 | 五折反柱体群 (D5d) | ||
| 特性 | |||
| 等角、复合 | |||
| 图像 | |||
| |||
顶点坐标
该复合多面体的顶点坐标拥有以下三种形式
- (±(3+4τ), 0, ±(4−3τ))
- (±(2−4τ), ±5τ, ±(1−2τ))
- (±(2+τ), ±5, ±(4+2τ))
τ = (1+√5)/2是 黄金比例 (有时作 φ)。
参考文献
- Skilling, John, Uniform Compounds of Uniform Polyhedra, Mathematical Proceedings of the Cambridge Philosophical Society, 1976, 79: 447–457, MR 0397554, doi:10.1017/S0305004100052440.