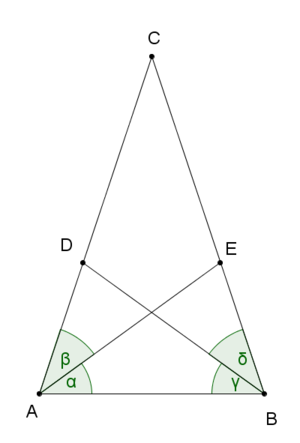
斯坦纳－雷姆斯定理

斯坦纳-雷姆斯定理说明：有三角形ABC，D、E点分别在AC、BC上，使得BD、AE分别为角ABC及角BAC的内角平分线。若BD=AE，则BC=AC。

${\displaystyle |AE|=|BD|,\,\alpha =\beta ,\,\gamma =\delta }$ ${\displaystyle \Rightarrow \triangle ABC}$是等腰三角形

类似的陈述适用于中线、高、内角n分线（将原来的角分成原来的1/n角的线段）和经过葛尔刚点（英语：Gergonne point）的线[1] （页面存档备份，存于互联网档案馆）等的塞瓦线段。可是这并不适用于外角平分线。一个132度、36度和12度的三角形是一个反例。

这个定理是德国数学家鲁道夫·雷姆斯（英语：C. L. Lehmus）（Ludolph Lehmus）向瑞士数学家雅各布·斯坦纳（英语：Jakob Steiner）提出的。