此条目没有列出任何参考或来源。 (2018年3月18日)
维基百科所有的内容都应该可供查证。请协助补充可靠来源以改善这篇条目。无法查证的内容可能会因为异议提出而移除。 |
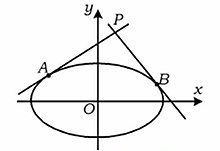
法国数学家加斯帕尔·蒙日发现:与椭圆 相切的两条垂直切线的交点的轨迹方程是
相切的两条垂直切线的交点的轨迹方程是 。这一结论被称为蒙日圆。
。这一结论被称为蒙日圆。
证明
设 分别为椭圆的左右焦点,焦距为 。设点 分别为点 关于 , 关于 的对称点。由椭圆的光学性质[a]知 , , 及 , , 分别三点共线,由椭圆定义有 。设 交直线 于点 , 交直线 于点 ,分别延长 , 交于点 ,则 , 。在矩形 中,由平面几何知识易知 ,于是 。
在双曲线中的结论
与双曲线 相切的两条垂直切线的交点的轨迹方程是 。
在抛物线中的结论
与抛物线 相切的两条垂直切线的交点的轨迹方程是 (可以看成是半径无穷大的圆)。
注释
- ^ 经过椭圆上一点的法线,平分这一点的两条焦点半径的夹角。