直角边

对于一个直角三角形，直角边（源自希腊字Κάθετος，复数Κάθετοι）；而英文的复数是catheti，是取自拉丁文cathetus的复数，常用的解释是"leg" ，即一个直角三角形中，形成90度的两条相邻的边。而余下的一条边，与直角相对，称为斜边。又因为毕氏定理在中文常被称为勾股定理或勾股弦定理，故在中文里，直角边常常被称为股，此乃延续中国古代的称呼。"leg"这种表达方式在多数情况之下并不常用，一般都用直角边或一个更迂回的说法：＂位于直角的一边＂。当提及到斜边，直角边一般被理解为余下的两边。

以图中的直角三角形为例，c₁ 和 c₂是直角边，而h便是斜边。

直角边的比例是三角函数中正切（tan）或余切（cot）的定义（视乎参考那一只角）。在直角三角形中，直角边的长度亦等于斜边的总长度与由直角用垂线分割斜边的线段的几何平均数。

对于一个不等腰的直角三角形，即一个任意的直角三角形，因为它的直角边有不同的长度，所以英文可以用"major"同"minor"来分辨。

对于等腰直角三角形，它的直角边便是其两腰。

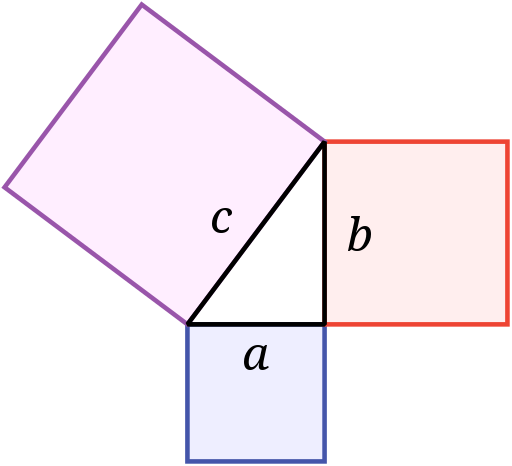
根据毕氏定理（又称勾股定理，毕达哥拉斯定理或勾股弦定理），两条直角边的平方之和是等于斜边的平方。同等地，以直角边为边长（见右图）所形成的正方形（a同b），它们的平方总和等于以斜边为边长所形成的正方形（c）之平方和。

图中由直角边为边长所形成的正方形，即蓝色同粉红色。它们的平方和会等于以斜边为边长所形成的正方形的平方和，即紫色。