兰姆位移
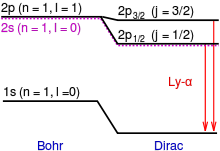
物理学中,以威利斯·兰姆(Willis Lamb)为名的兰姆位移(Lamb shift)是氢原子两个能级(与)间的微小能量差。根据狄拉克的量子理论,量子数及量子数相同但量子数不同的氢原子能态应该是简并态,也就是不会有能量差值。[1]:332-333
实验成果
于1947年,兰姆以及罗伯特·雷瑟福(Robert Retherford)进行了一项实验,利用微波技术来刺激氢原子 与 能级之间的射频跃迁(radio-frequency transitions)。利用比光学跃迁(optical transitions)还要低的频率,使得多普勒增宽(Doppler broadening)效应可以被忽略(因为多普勒谱线增宽跟频率呈正比关系)。他们两人发现如此使得 能级比 能级还高出约1057兆赫(MHz)的能量差。
如此特殊的差异是量子电动力学中的单圈效应(one-loop effect),可以解释为被原子发射又再吸收的虚光子所造成的影响。在量子电动力学中,电磁场也被量子化,而类似于量子力学中的量子谐振子,其最低能态所具有的能量不会是零。因此存在微小的零点振荡,导致电子会进行快速的振荡运动(参见颤动条目)。电子云因此有些“抹开”("smeared out"),而半径从 变为 。
库仑位势因此被摄动了一些,而两能级的简并性被破坏掉。新的场势可以(利用原子单位)近似为:
兰姆位移本身则可写为
- ,针对
其中约为13的 随着 些微变动;而
- ,针对 以及
其中 为一个小的数值(< 0.05)。
氢原子谱线中的兰姆位移
于1947年,汉斯·贝特(Hans Bethe)首次对氢原子谱线中的兰姆位移做出解释,并且对导引出量子电动力学的进程建下基础。兰姆位移目前对于精细结构常数α的测量提供了比百万分之一还佳的精确度,使得量子电动力学预测的正确性得到证实。
参见
- 威利斯·兰姆
- 塞曼效应 -- 用于衡量兰姆位移
- 量子退火
- 量子泡沫
- 黑洞辐射
参考文献
- ^ Kragh, Helge. Quantum Generations: A History of Physics in the Twentieth Century Reprint. Princeton University Press. 2002. ISBN 978-0691095523.
外部链接
- Hans Bethe talking about Lamb-shift calculations (页面存档备份,存于互联网档案馆) on Web of Stories
- Nobel Prize biography of Willis Lamb (页面存档备份,存于互联网档案馆)
- Nobel lecture of Willis Lamb: Fine Structure of the Hydrogen Atom (页面存档备份,存于互联网档案馆)