范德科皮特序列(英语:van der Corput sequence)是定义在单位区间上的一维低差异序列,由荷兰数学家约翰内斯·范德科皮特于1935年提出。将以基数b表示的自然数列反转后便可得到范德科皮特序列。
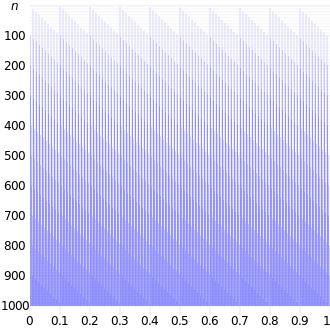
以10为基数的范德科皮特序列前
n项(
n从0至999)的图示
使用基数b可将自然数n表示为

其中第k位为dk(n),满足0 ≤ dk(n) < b。
由此,可以得到范德科皮特序列的第n位:

例如,以10为基数的范德科皮特序列的前几项为

而以2为基数的范德科皮特序列的前几项则为

参考文献
- van der Corput, J.G., Verteilungsfunktionen. I. Mitt., Proc. Akad. Wet. Amsterdam, 1935, 38: 813–821, Zbl 0012.34705 (德语)
- Kuipers, L.; Niederreiter, H., Uniform distribution of sequences, Dover Publications: 129,158, 2005 [1974], ISBN 0-486-45019-8, Zbl 0281.10001




