凸组合

在凸几何（英语：Context geometry）领域，凸组合（英语：convex combination）指点的线性组合，要求所有系数都非负且和为 1。此处的“点”可以是仿射空间中的任何点，包括向量和标量。

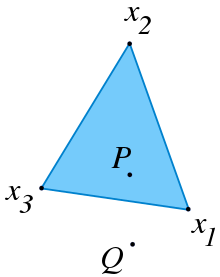
平面中有三个点 ${\displaystyle x_{1},x_{2},x_{3}}$，点 ${\displaystyle P}$ 是这三个点的一种凸组合，而点 ${\displaystyle Q}$ 不是。

（${\displaystyle Q}$ 是这三个点的一种仿射组合（英语：Affine combination））

如果给出有限个实向量空间中的点 ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ 这些点的凸组合即一个这样的点：

${\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}}$

其中的任意实数 ${\displaystyle a_{i}}$ 都满足 ${\displaystyle a_{i}\geq 0}$，且 ${\displaystyle a_{1}+\dots +a_{n}=1}$。

任意两个点的凸组合都在它们之间的线段上。

点集的凸包等价于该点集的所有凸组合。