F-分布
在概率论和统计学里,F-分布(F-distribution)是一种连续概率分布,[1][2][3][4]被广泛应用于似然比率检验,特别是ANOVA中。
|
概率密度函数 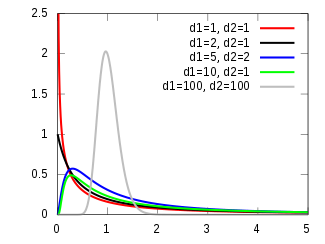 | |||
|
累积分布函数 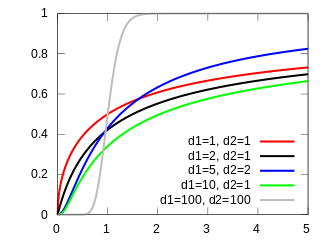 | |||
| 参数 | 自由度 | ||
|---|---|---|---|
| 值域 | |||
| 概率密度函数 | |||
| 累积分布函数 | |||
| 期望值 | for | ||
| 众数 | for | ||
| 方差 | for | ||
| 偏度 |
for | ||
| 峰度 | 见下文 | ||
定义
如果随机变量 X 有参数为 d1 和 d2 的 F-分布,我们写作 X ~ F(d1, d2)。那么对于实数 x ≥ 0,X 的概率密度函数 (pdf)是
这里 是B函数。在很多应用中,参数 d1 和 d2 是正整数,但对于这些参数为正实数时也有定义。
其中 I 是正则不完全贝塔函数。
- .
特征
其中:
- U1和U2呈卡方分布,它们的自由度(degree of freedom)分别是d1和d2。
- U1和U2是相互独立的。
参见
- F检验
参考文献
- ^ Johnson, Norman Lloyd; Samuel Kotz; N. Balakrishnan. Continuous Univariate Distributions, Volume 2 (Second Edition, Section 27). Wiley. 1995. ISBN 0-471-58494-0.
- ^ Abramowitz, Milton; Stegun, Irene Ann (编). Chapter 26. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series 55 Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first. Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. 1983: 946. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253. 已忽略未知参数
|orig-date=(帮助) - ^ NIST (2006). Engineering Statistics Handbook – F Distribution (页面存档备份,存于互联网档案馆)
- ^ Mood, Alexander; Franklin A. Graybill; Duane C. Boes. Introduction to the Theory of Statistics (Third Edition, pp. 246–249). McGraw-Hill. 1974. ISBN 0-07-042864-6.











