卡尔曼猜想

卡尔曼猜想（Kalman's conjecture）或卡尔曼问题（Kalman problem）是已找到反例的猜想，是针对非线性控制系统，其中有一个标量非线性元素，此系统在线性稳定区间内的绝对稳定性。卡尔曼猜想是阿依热尔曼猜想的加强版本，也是Markus–Yamabe猜想（英语：Markus–Yamabe conjecture）的特例。卡尔曼猜想虽已证实为否，不过带出了（有效的）绝对稳定性的充份准则。

图1：控制系统的方块图，其中的G(s)是线性传递函数，而f(e)是单值连续可微的函数

卡尔曼猜想的数学描述（卡尔曼问题）

鲁道夫·卡尔曼在1957年的论文[1]中提到：

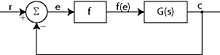
若图1中的f(e)用e乘上常数K取代，K对应f'(e)中所有的可能值，发现闭回路系统在所有K值下都收敛。在直觉上会认为此系统是单调稳定的，也就是说，所有暂态的解都会收敛到唯一、稳定的临界点。

卡尔曼的描述可以写成以下的猜想[2]：

考虑一个有单一标量非线性函数的函数

 

其中P是常数的n×n矩阵，q、r是常数的n维向量，∗是转置符号，f(e)是标量函数，f(0) = 0。假设，f(e)是可微分函数，而且满足以下条件

 

。则卡尔曼猜想是指此系统在大区域稳定（也就是其唯一驻点为全域吸引子）若配合f(e) = ke, k ∈ (k1, k2)的所有线性系统都是渐近稳定。

阿依热尔曼猜想要求非线性导数的条件，而卡尔曼猜想要求非线性本身要在线性区间内。

卡尔曼猜想在n ≤ 3时成立，若是n > 3，存在有效生成反例的作法[3][4]：非线性的导数在线性稳定区间内，存在唯一稳定的平衡点，以及一个稳定的周期解（隐蔽振荡）。

在离散系统下，卡尔曼猜想只在n=1时成立，在n ≥ 2时可以建构反例[5][6]。

参考资料

  1. ^ Kalman R.E. Physical and Mathematical mechanisms of instability in nonlinear automatic control systems. Transactions of ASME. 1957, 79 (3): 553–566. 
  2. ^ Leonov G.A.; Kuznetsov N.V. Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems (PDF). Doklady Mathematics. 2011, 84 (1): 475–481 [2019-05-11]. doi:10.1134/S1064562411040120. （原始内容存档 (PDF)于2016-03-04）. 
  3. ^ Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits (PDF). Journal of Computer and Systems Sciences International. 2011, 50 (5): 511–543 [2019-05-11]. doi:10.1134/S106423071104006X. （原始内容存档 (PDF)于2016-03-04）. 
  4. ^ Leonov G.A.; Kuznetsov N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. International Journal of Bifurcation and Chaos. 2013, 23 (1): art. no. 1330002 [2019-05-11]. doi:10.1142/S0218127413300024. （原始内容存档于2019-03-24）. 
  5. ^ Carrasco J.; Heath W. P.; de la Sen M. Second-order counterexample to the Kalman conjecture in discrete-time. 2015 European Control Conference. 2015. 
  6. ^ Heath W. P.; Carrasco J; de la Sen M. Second-order counterexamples to the discrete-time Kalman conjecture. Automatica. 2015. doi:10.1016/j.automatica.2015.07.005. 

延伸阅读

外部链接