极点 (复分析)

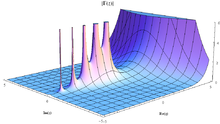
假设${\displaystyle U}$  是复平面${\displaystyle \mathbb {C} }$ 的开子集，${\displaystyle a}$ 是${\displaystyle U}$ 的一个元素，${\displaystyle f:U-\{a\}\to \mathbb {C} }$ 是一个在定义域内全纯的函数。如果存在一个全纯函数${\displaystyle g:U\to \mathbb {C} }$ 和一个非负整数${\displaystyle n}$ ，使得对于所有${\displaystyle U-\{a\}}$ 内的${\displaystyle z}$ ，都有

${\displaystyle f(z)={\frac {g(z)}{(z-a)^{n}}}}$ 

那么${\displaystyle a}$ 便称为${\displaystyle f}$ 的极点。满足以上条件的最小整数${\displaystyle n}$ 称为极点的阶。一阶的极点又称为简单极点。

1.函数f在极点a的极限值是${\displaystyle \infty }$ .也就是说

${\displaystyle \lim _{z\rightarrow a}f(z)=\infty }$ 

2.由性质1.可知,如果令函数

${\displaystyle h(z)={\frac {1}{f(z)}}}$ 

那么代入定义可知：

${\displaystyle h(z)=(z-a)^{m}{\frac {1}{g(z)}}}$ 

其中${\displaystyle {\frac {1}{g(z)}}}$ 在${\displaystyle z=a}$ 点解析。那么有${\displaystyle z=a}$ 是${\displaystyle h(z)}$ 的m阶零点。

3.由于${\displaystyle g}$ 是全纯函数，${\displaystyle f}$ 可以表示为：

${\displaystyle f(z)={\frac {a_{-n}}{(z-a)^{n}}}+\cdots +{\frac {a_{-1}}{(z-a)}}+\sum _{k\geq 0}a_{k}(z-a)^{k}.}$ 

这是一个洛朗级数，它的主部分是有限的。全纯函数${\displaystyle \sum _{k\geq 0}a_{k}(z-a)^{k}}$ 称为${\displaystyle f}$ 的正则部分。因此，点${\displaystyle a}$ 是${\displaystyle f}$ 的${\displaystyle n}$ 阶极点，当且仅当${\displaystyle f}$ 在${\displaystyle a}$ 处的罗朗级数中所有低于${\displaystyle -n}$ 的次数都为零，而${\displaystyle -n}$ 次项不为零。

如果函数${\displaystyle f}$ 的一阶导数在${\displaystyle a}$ 处具有简单极点，则${\displaystyle a}$ 是${\displaystyle f}$ 的一个分支点（英语：Branch point），但反过来不成立。

一个既不是极点又不是分支点的非可去奇点称为本性奇点。

除了一些孤立奇点外全纯的函数，且所有的奇点均为极点，则该函数称为亚纯函数。

• 零点
• 留数

• 埃里克·韦斯坦因. Pole. MathWorld. 
• 零点和极点的教程