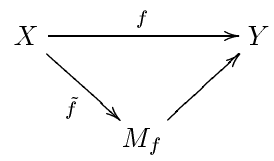
构造
Mf 的正式定义如下:
-
这里 是单位区间, 表示两个拓扑空间的不交并, 是把 与 等同起来的等价关系(将柱 的一个底面通过 f 与 Y 黏合起来)。
从而非正式地说,映射柱 是把 的一个底面用 f 黏贴到 Y 得到的构造。
定义 为 (将 X 包含到另一个底面)。定义 为 而在 Mf 的 Y 部分为恒同。根据等价关系 ~ 这是良定义的。
注意到 Y 是 的形变收缩。
投影 分裂(通过 ),形变收缩(取时间参数为 s)由下式给出:
-
(这里所有 Y 中的点不动,从而是一个形变收缩。)
应用
映射柱将关于子空间或空间包含的定理运用到到不必是单射的一般映射。
因此,那些与空间、所涉及映射的同伦类无关的定理或方法(比如同调、上同调或同伦理论本身)可能可适用到 ,这里假设 以及 事实上是子空间的包含。另外,这个构造更本质的吸引之处是它与通常心理的印象一个函数是将 中的点“送到” 中的点一致,从而 嵌入 中也是(尽管函数不必是一对一的)。这个构造给出了一个图像同伦等价于直觉的那个,这表明直觉图像是正确的只要 的形变不是一个阻碍。
范畴应用与解释
我们可以用映射柱构造同伦极限:给定一个图表,将其中的映射用上纤维化代替(利用映射柱),然后取通常的逐点极限(需多些注意,但映射柱是其中一部分)。
相反地,映射柱是图表的同伦推出,这里 而 。
映射望远镜
给定映射序列
-
映射望远镜是同伦正向极限。如果所有这些映射已经是上纤维化(比如正交群 ),则正向极限是并集,但是一般情形必须使用映射望远镜。映射望远镜是一个映射柱序列,底面和底面相连。这个构造的图像看起来像堆起来的变大的柱子,即像一个望远镜,从而有这样的名称。
映射望远镜的正式定义为
-
和同伦(同调)等价的关系
一个映射 是一个同伦等价,当且仅当它的映射柱可缩。
设 设一个固定的同调理论。映射 诱导了 上的同构,当且仅当映射 诱导了 上的同构,即 。
另见
参考文献