戴德金η函数

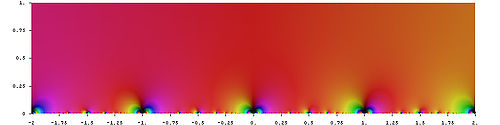
戴德金η函数（Dedekind eta function）是定义在上半平面的全纯函数，这是权1/2的模形式之一例。

η函数的描绘

对每个属于上半平面的复数${\displaystyle \tau }$，置${\displaystyle q=e^{2\pi i\tau }}$，则η函数表为

${\displaystyle \eta (\tau )=q^{1/24}\prod _{n=1}^{\infty }(1-q^{n})}$

η函数满足以下函数方程：

• ${\displaystyle \eta (\tau +1)=\exp({\frac {2\pi i}{24}})\eta (\tau )}$
• ${\displaystyle \eta (-1/\tau )={\sqrt {\frac {\tau }{i}}}\eta (\tau )}$

此处的根号是方根函数在右半平面的解析延拓

${\displaystyle re^{i\theta }\mapsto r^{1/2}e^{i\theta /2},\quad |\theta |<\pi /2}$。

一般而言，对${\displaystyle a,b,c,d\in \mathbb {Z} ,ab-cd=1}$，我们有

${\displaystyle \eta \left({\frac {a\tau +b}{c\tau +d}}\right)=\epsilon (a,b,c,d)\left(-i(c\tau +d)\right)^{1/2}\eta (z)}$

其中的自守因子${\displaystyle \epsilon }$定为

${\displaystyle \epsilon (a,b,c,d)=\exp i\pi \left({\frac {a+d}{12c}}+s(-d,c)\right)}$。

而${\displaystyle s(h,k)}$为戴德金和

${\displaystyle s(h,k)=\sum _{n=1}^{k-1}{\frac {n}{k}}\left({\frac {hn}{k}}-\left\lfloor {\frac {hn}{k}}\right\rfloor -{\frac {1}{2}}\right)}$

由此函数方程可知η是权1/2的模形式，因此可由η构造更多的模形式，例如魏尔施特拉斯的模判别式即可表为

${\displaystyle \Delta (\tau )=(2\pi )^{12}\eta (\tau )^{24}}$。

事实上，由函数方程可知${\displaystyle \eta ^{24}}$是权12的模形式，而这类模形式构成复一维向量空间，比较傅里叶展开的常数项，上式立可得证。

拉马努金有一个著名的猜想：在傅立叶展开式中，对任一素数，的系数的绝对值恒。此猜想最后由德利涅证明。

上述诸例点出了模形式与若干古典数论问题的联系，例如以二次型表示整数以及整数分拆问题。赫克算子（英语：Hecke operator）理论阐释了模形式与数论的关键联系，同时也联系了模形式与表示理论。