阿拉-萨拉姆-迟哈剌多项式
阿拉-萨拉姆-迟哈剌多项式(Al-Salam-Chihara polynomials)是一个以基本超几何函数定义的正交多项式[1]
极限关系
阿拉-萨拉姆-迟哈剌多项式→连续q拉盖尔多项式
令阿拉-萨拉姆-迟哈剌多项式 b=0,即得连续大Q埃尔米特多项式
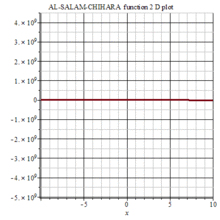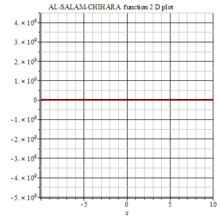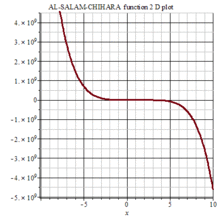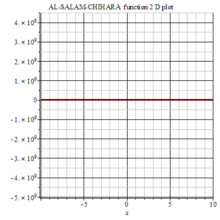
图集
参考文献
- ^ Roelof KoeKoek, Hypergeometric Orthogonal Polynomials and its q-Analogues, p455,Springer 2010
- Al-Salam, W. A.; Chihara, Theodore Seio, Convolutions of orthonormal polynomials, SIAM Journal on Mathematical Analysis, 1976, 7 (1): 16–28, ISSN 0036-1410, MR 0399537, doi:10.1137/0507003
- Gasper, George; Rahman, Mizan, Basic hypergeometric series, Encyclopedia of Mathematics and its Applications 96 2nd, Cambridge University Press, 2004, ISBN 978-0-521-83357-8, MR 2128719, doi:10.2277/0521833574
- Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F., Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, 2010, ISBN 978-3-642-05013-8, MR 2656096, doi:10.1007/978-3-642-05014-5
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F., Al-Salam–Chihara polynomials, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248