数学中,黎曼ξ函数(英语:Riemann Xi function)是黎曼ζ函数的变型,其定义是为了得到一个简单的泛函方程式。此函数得名于波恩哈德·黎曼。
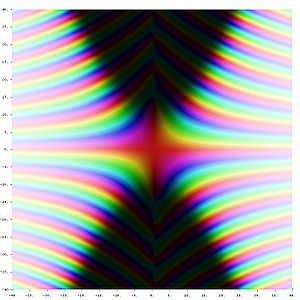
复平面中的黎曼ξ函数

。
复平面中的点

,其色彩代表了该点的函数值;较暗的颜色表示其值接近于零,而色调表示了函数值的
幅角。
定义
爱德蒙·兰道将黎曼原先小写的ξ函数以被改为大写的Ξ函数(另参见下方),而兰道的小写ξ函数则定义为:[1]
- ,
其中
- ;
- ζ(s)为黎曼ζ函数;
- Γ(s)为伽玛函数。
兰道的小写ζ函数的泛函方程式(或称反射式)为
- 。
兰道的大写Ξ函数(loc. cit., §71)为
-
遵守泛函方程式:
- 。
一如兰道所写(loc. cit., p. 894),Ξ函数即原先的黎曼ξ函数。
函数值
当s为偶数,亦即s = 2n,ξ(s)一般式为
-
其中Bn为第n个伯努利数。
例如:
-
级数表示式
其中
相关条目
参考文献
- ^ Edmund Landau. Handbuch der Lehre von der Verteilung der Primzahlen, Teubner, Leipzig 1909. Third edition Chelsea, New York, 1974, §70.


