此条目没有列出任何参考或来源。 (2022年5月10日)
维基百科所有的内容都应该可供查证。请协助补充可靠来源以改善这篇条目。无法查证的内容可能会因为异议提出而移除。 |
平分线是一条能将一条线段二等分的线。
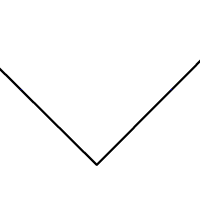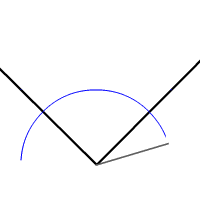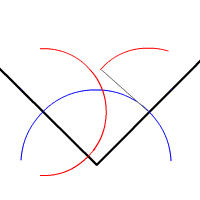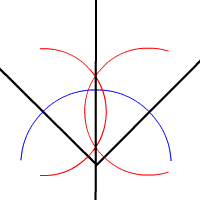
角平分线是将两条线相交所夹的角二等分的线。
角平分线的性质
角平分线上的任意一点,到角两边的距离相等。
即如图所示:
平分 为 上一点 于 于
则
该性质的证明
利用三角形全等,可以很容易推得此结论。
下面作一下简单推导。
平分
在 与 中
证毕。
角平分线的判定
判定
与其性质相对应的,就是角平分线的判定:
若有一点至角两边距离相等,则该点在该角的角平分线上。
即:
已知 为 上一点
如果 那么 平分
证明
在 与 中
平分
证毕。
内心
任意三角形ABC中, 、 、 角平分线交于一点I,则我们称此点I为三角形ABC的内心。
三角形的内心恒在图形内部,且到三角形之三边距离等长
参见