焦点 (几何)

用二个焦点定义圆锥曲线

椭圆可以定义为平面上到两个固定点（焦点）的距离之和为常数的点之轨迹。

圆是一种特殊的椭圆，其二个焦点重合，只剩一个焦点。因此圆可以定义为平面上到一个固定点的距离为常数的点之轨迹。圆也可以用阿波罗尼斯圆（英语：Circles of Apollonius）的方式定义，定义成和二个焦点距离有固定比例的点之轨迹，会出现二个不同的轨迹。

抛物线是一种特殊的椭圆，其中一个焦点在无穷远处。

双曲线也可以用二个焦点来定义，是两个焦点的距离差（的绝对值）是常数的点的轨迹。

用焦点和准线定义圆锥曲线

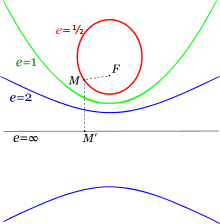
也可以用一个焦点和一条准线（directrix）定义圆锥曲线，准线是不通过焦点的直线。圆锥曲线是距焦点距离和距准线距离比例为一定值的线，此定值即为偏心率e。若e在0到1之间，此圆锥曲线为椭圆，若e=1，此圆锥曲线为抛物线，若e大于1，此圆锥曲线为双曲线。若到焦点的距离固定，准线为无穷远线，偏心率为零，此圆锥曲线就是圆。

天文学的重要性

在重力场的二体问题中，二个物体相对于彼此的轨道可以用二个重叠的圆锥曲线表示，二个圆锥曲线的都会有焦点落在二个物体的共同质量中心（质心）。

例如，微型行星冥王星的最大卫星冥卫一其轨道为椭圆，其中一个焦点在冥王星－冥卫一双星系统的质心上，而冥王星的的轨道为椭圆，其中一个焦点也是在双星系统的质心上，如动画,中所述。

而地球的卫星月球轨道的椭圆，也有一个焦点在地球－月球双星系统的质心上，但此质心在地球内部，而地球（或说是地球的质心）也绕着椭圆轨道运转，而一个焦点也在地球－月球双星系统的质心上。

而冥王星－冥卫一系统也在另一个椭圆轨道上运行，此椭圆的一个焦点是冥王星、冥卫一和太阳的质心，而地球－月球系统也是在另一个类似的椭圆轨道上运行。这些质心都在太阳的内部。

二颗联星也会绕着其共同质心，在椭圆轨道上运行。

• Hilton, Harold. Plane Algebraic Curves. Oxford. 1920: 69.