六维正七胞体
在几何学中,六维正七胞体(heptapeton[1]:127)是一种自身对偶的正六维多胞体[2],是六维空间中的单纯形[3],又称为6-单纯形(6-simplex)[4],由7个五维正六胞体组成,其二面角为cos−1(1/6)约为80.41°。[2]
| 正七胞体 | |
|---|---|
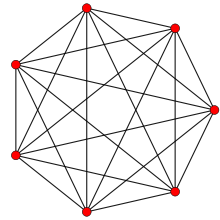 | |
| 类型 | 正六维多胞体 七胞体 |
| 家族 | 单纯形 |
| 维度 | 六维 |
| 对偶多胞形 | 正七胞体(自身对偶) |
| 识别 | |
| 名称 | 正七胞体 |
| 鲍尔斯缩写 | hop |
| 数学表示法 | |
| 考克斯特符号 | |
| 施莱夫利符号 | {3,3,3,3,3} {35} |
| 性质 | |
| 五维胞 | 7个五维正六胞体 |
| 四维胞 | 21个正五胞体 |
| 胞 | 35个正四面体 |
| 面 | 35个正三角形 |
| 边 | 21 |
| 顶点 | 7 |
| 欧拉示性数 | 0 |
| 特殊面或截面 | |
| 皮特里多边形 | 正七边形 |
| 组成与布局 | |
| 顶点图 | 五维正六胞体 |
| 对称性 | |
| 对称群 | A6 [35], 5040阶 |
性质
六维正七胞体共有7个顶点、21条边、35个三角形的面、35个四面体的胞、21个四维正五胞体的四维胞和7个五维正六胞体的五维胞组成[5],其中五维正六胞体为六维正七胞体的维面。对于一个边长为a的六维正七胞体,其超胞积是 ,表胞积是 ,高是 。 若一个六维正七胞体的棱长为1,则其外接六维超球的半径为 ,内切六维超球的半径为 。[2]
作为一种排布
六维正七胞体的排布矩阵为:[2]
行和列对应于六维正七胞体的顶点、边、面、胞、四维胞、五维胞。对角线上的数字表示该元素在六维正七胞体中的数量。非对角线的数量表示对应行所代表的元素上有多少列所代表的元素交于该处。由于六维正七胞体是一种自身对偶的多胞体,因此这个排布矩阵旋转180度后会相同。[7][8]
顶点坐标
若一个六维正七胞体几何中心位于原点,且边长为2单位长,则其顶点坐标为:
图像
| Ak考克斯特平面 | A6 | A5 | A4 |
|---|---|---|---|
| 图像 | |||
| 二面体群对称性 | [7] | [6] | [5] |
| Ak考克斯特平面 | A3 | A2 | |
| 图像 | |||
| 二面体群对称性 | [4] | [3] |
参考文献
- ^ 2.0 2.1 2.2 2.3 Klitzing, Richard. heptapeton. bendwavy.org. [2022-06-02]. (原始内容存档于2021-09-30).
- ^ Ufuoma, Okoh and Ikhile, Agun. On Simplicial Polytopic Numbers. Asian Research Journal of Mathematics. 2019-06: 1–20. doi:10.9734/arjom/2019/v14i230122.
- ^ Joshua Lande. Fitting The Unknown (PDF). slac.stanford.edu. 2010-09-01 [2022-06-02]. (原始内容 (PDF)存档于2015-10-09).
- ^ Ferretti, Elena. The algebraic formulation: Why and how to use it. Curved and Layered Structures (De Gruyter Open). 2015, 2 (1).
- ^ Coxeter, H.S.M. Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5). [[:正多胞形 (書籍)|Regular Polytopes]] 3rd. Dover. 1973: 296. ISBN 0-486-61480-8. 网址-维基内链冲突 (帮助)
- ^ Coxeter 1973[6], §1.8 Configurations
- ^ Coxeter, H.S.M. Regular Complex Polytopes 2nd. Cambridge University Press. 1991: 117. ISBN 9780521394901.