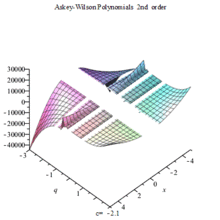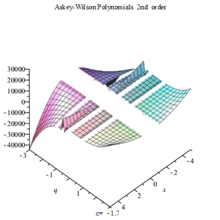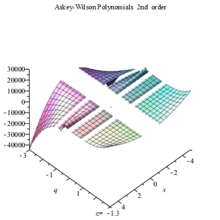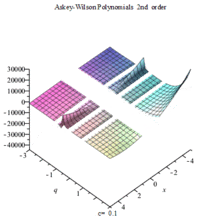
阿斯基-威尔逊多项式
阿斯基-威尔逊多项式是一个以基本超几何函数表示的正交多项式:
其中 阿斯基-威尔逊多项式是威尔逊多项式的q模拟.
极限关系
在阿斯基-威尔逊多项式中,令 即得连续双哈恩多项式[1]
在阿斯基-威尔逊多项式中作代换 , , , , 即得连续q哈恩多项式:
- 阿斯基-威尔逊多项式→大q雅可比多项式
参考文献
- ^ Roelof,p420
Roelof KoekoeK,Peter Lesky Rene Swarttouw,Hypergeometric Orthogonal Polynomials and Their q-Analogues, Springer 2010*Askey, Richard; Wilson, James, Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials, Memoirs of the American Mathematical Society, 1985, 54 (319): iv+55, ISBN 978-0-8218-2321-7, ISSN 0065-9266, MR 0783216, doi:10.1090/memo/0319
- Gasper, George; Rahman, Mizan, Basic hypergeometric series, Encyclopedia of Mathematics and its Applications 96 2nd, Cambridge University Press, 2004, ISBN 978-0-521-83357-8, MR 2128719
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F., Askey-Wilson class, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248
- Koornwinder, Tom H., Askey-Wilson polynomial, Scholarpedia, 2012, 7 (7): 7761, doi:10.4249/scholarpedia.7761 外部链接存在于
|title=(帮助)