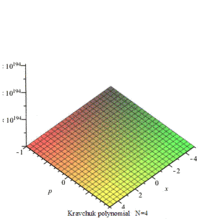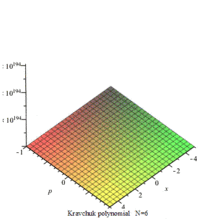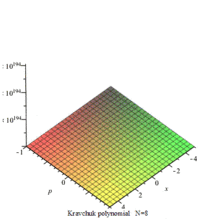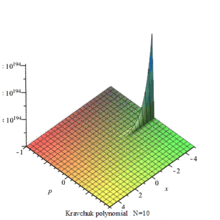
克拉夫楚克多项式

克拉夫楚克多项式以超几何函数定义如下

Kravchuk polynomials animation

$K_{n}(x;p,N)={N \choose n}^{-1}*$ $\sum _{k=0}^{n}{N-x \choose n-k}*{x \choose k}*(1-1/p)^{k}$ = $_{2}F_{1}(-n,-x;N;1/p)$

克拉夫楚克多项式的头几项是

$K_{0}(x,p,N)=1$

$K_{1}(x,p,N)=1-{\frac {x}{p*N}}$

$K_{2}(x,p,N)=1+({\frac {-2}{p*N}}+{\frac {1}{(p^{2}*N*(-N+1)}})*x-{\frac {x^{2}}{(p^{2}*N*(-N+1))}}$

$K_{3}(x,p,N)=1+({\frac {-3}{(p*N)}}+{\frac {3}{(p^{2}*N*(-N+1))}}-{\frac {2}{(p^{3}*N*(-N+1)*(-N+2))}})*x+(-3/(p^{2}*N*(-N+1))+3/(p^{3}*N*(-N+1)*(-N+2)))*x^{2}-x^{3}/(p^{3}*N*(-N+1)*(-N+2))$

极限关系

量子Q克拉夫楚克多项式→ 克拉夫楚克多项式：

$\lim _{a\to 1}=K_{n}^{qtm}(q^{-}{x};p,N;q)=K_{n}(x;p^{-1},N)$

令双Q克拉夫楚克多项式 $c=1=p^{-1}$ ,并令q→1,即得克拉夫楚克多项式

参考文献

Kravchuk, M., Sur une généralisation des polynomes d'Hermite., Comptes Rendus Mathematique, 1929, 189: 620–622, JFM 55.0799.01 （法语）
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F., Hahn Class: Definitions, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248
Nikiforov, A. F.; Suslov, S. K.; Uvarov, V. B., Classical Orthogonal Polynomials of a Discrete Variable, Springer Series in Computational Physics, Berlin: Springer-Verlag, 1991, ISBN 3-540-51123-7, MR 1149380 .
Levenshtein, Vladimir I., Krawtchouk polynomials and universal bounds for codes and designs in Hamming spaces, IEEE Transactions on Information Theory, 1995, 41 (5): 1303–1321, MR 1366326, doi:10.1109/18.412678 .
F. J. MacWilliams; N. J. A. Sloane, The Theory of Error-Correcting Codes, North-Holland, 1977, ISBN 0-444-85193-3