赝矢量
赝矢量(英语:Pseudovector)也称为伪向量,指的是在瑕旋转下,除了随之反射外,还会再上下翻转的矢量(因为右手定则的关系)。矢量(极矢量)和赝矢量(轴矢量)都是广义上的矢量,在一般旋转下的特性相同。但更严格地说,矢量还要求在瑕旋转下,除了空间反演外,不会再改变方向。
在三维空间中,赝矢量p可以表示为二个极矢量a和b的外积:[2]
以此方式计算的p是赝矢量,其中一个例子是有向平面的法向量。有向平面可以用二个不平行的向量a和b来定义[3]。向量a × b垂直此平面(和平面垂直的向量有二个,其方向恰好相反,可以用右手定则决定是哪一个),为一赝矢量。
许多物理量是赝矢量,例如磁感应强度、角速度等。在数学上,赝矢量是三维的二重向量,可以由此推得赝矢量的变换规则。n维几何代数的赝矢量是n − 1维代数的元素,可以表示为Λn−1Rn。可以由赝矢量引申出赝标量及赝张量,在瑕旋转下会比标量及张量多出一个负号。
物理例子
物理中赝矢量的例子包括有磁场、力矩、涡量及角动量。
考虑赝矢量角动量 L = r × p。假设开一部车前进,各轮子产生的角动量会朝左。若考虑车子的镜像,角动量向量若以一般向量的观点来看,其镜像应该往右,但真正车子镜像的角动量仍然往左(在镜像中的车轮仍然往前进),因此在赝矢量反射后,会比一般向量多一个负号。
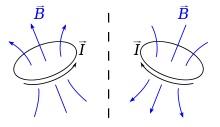
矢量和赝矢量之间的不同在研究物理系统的对称性时很重要。考虑在一个z = 0平面上的线圈,上面有电流,会产生一个z方向的磁场,此系统在z平面的镜相反射下是对称(不变)的,磁场不会因镜相反射而相反,但是若将磁场视为一个一般的向量,应该会随镜相反射而相反,其原因就是因为磁场是赝矢量,产生一个额外的负号,因为没有反向。
相关条目
参考资料
- ^ Stephen A. Fulling, Michael N. Sinyakov, Sergei V. Tischchenko. Linearity and the mathematics of several variables. World Scientific. 2000: 343. ISBN 981-02-4196-8.
- ^ Aleksandr Ivanovich Borisenko, Ivan Evgenʹevich Tarapov. Vector and tensor analysis with applications Reprint of 1968 Prentice-Hall. Courier Dover. 1979: 125 [2014-08-20]. ISBN 0-486-63833-2. (原始内容存档于2016-12-22).
- ^ RP Feynman: §52-5 Polar and axial vectors (页面存档备份,存于互联网档案馆) from Chapter 52: Symmetry and physical laws, in: Feynman Lectures in Physics, Vol. 1