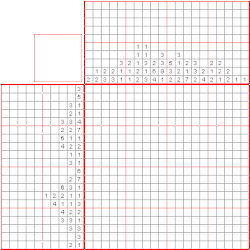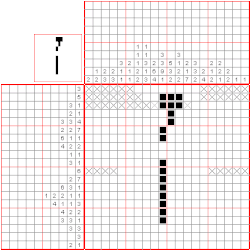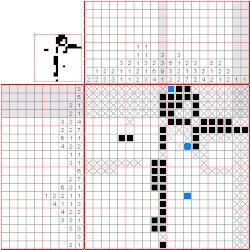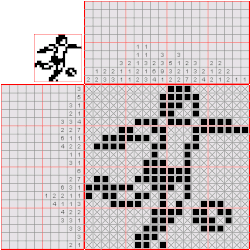
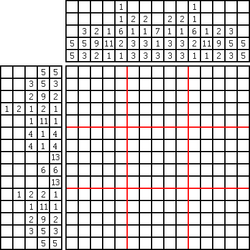
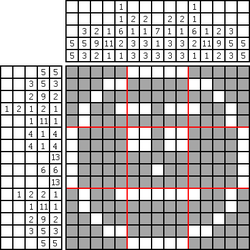
数织

数织是一种逻辑游戏，以猜谜的方式绘画黑白位图。在一个网格中，每一行和列都有一组数，玩家需根据它们来填满或留空格子，最后就可以由此得出一幅图画。例如，“4 8 3”的意思就是指该行或列上有三条独立的线，分别占了4、8和3格，而每条线最少要由一个空格分开。传统上，玩家是以黑色填满格子，和以“×”号标记一定不需要填充的格子。数织是一个NP完全的问题。

动画化的解谜过程
问题
答案

数织是在1987年由日本人西尾彻也发明的。数织的日文名称是“お絵かきロジック”，意思是“绘画逻辑”。数织初见于日本的谜题杂志，玩家用纸和笔来玩。随后，任天堂以“Mario's Picross”为名推出了两款Game Boy和九款超级任天堂游戏。现时NDS上亦有名为Picross DS的同款游戏。2015年十二月，任天堂推出了名为“Pokemon Picross”的3DS游戏。

名字

Nonogram有着许多不同的名字，包括Paint by Numbers、Griddlers、Pic-a-Pix、Picross、Pixel Puzzles、Crucipixel、Edel、FigurePic、Grafilogika、Hanjie、Illust-Logic、Japanese Crosswords、Japanese Puzzles、Kare Karala!、Logic Art、Logic Square、Logicolor、Logik-Puzzles、Logimage、Zakókodované obrázky、Maľované krížovky、Oekaki Logic、Oekaki-Mate、Paint Logic、Shchor Uftor和Tsunami。

Nonogram至今还未有正式或广泛流传的中文名称，已知的中文名有：数织、数墙、填方块、发现小花、逻辑拼图、津波拼图等。

解谜技巧

尽量的填充

玩家可以利用数组尽量的填充格子。

如果数字等于行高或列寛的话，该行所有格子都要填满。

如果不是的话，玩家则可以假设每条线只有由一个空格分隔，把线组推到可移动的空间的最尽；然后，把线组推到另一个尽头。两者重叠的填充部分就是一定要填充的格子。

例如：

8
8

可得出这结论：

8

又例如：

4 3
4 3

可得出这结论：

4 3

尽量的标空

除了尽量的填充之外，玩家亦可以把一定不可能要填上的空格用“×”号标记起来，从而减少需要考虑的格子。

如果数字是零的话，该行所有格子都需留空（玩家可用“×”号标上）。

即使不是零，玩家也可以根据已填充的格子，把线推到可移动的空间的最尽，再把线推到另一尽头。两者重叠的留空部分就是一定不需要填上的空格。

假设玩家因为之前的推算，现已得出以下结果：

3 1

如果把线填满，可以有以下两个极端的可能性：

3 1
3 1

因此可得出这结论：

3 1 × × × ×

又如果该行或列中有些空格已经不足之放上任何一条线，那些空格也是可以标空的。例如：

3 × ×

玩家可以不用考虑右边的空格：

3 × × × × × ×

连接或分离邻近的线

如果两条邻近的线由一个空格分隔的话，玩家可以用以下的推论尝试把它填充或标空：

  • 如果把它们连接起来，会令线条过长的话，该空格应该标空。
  • 如果把它们分隔，会令线条数目过多的话，该空格应该填充。

例子如下：

5 2 2

经过推论后：

5 2 2 ×

因为需要尽量的填充和标空，聪明的玩家在这例子可能会直接跳到这步：

5 2 2 × × × × × ×

利用矛盾推论

在一些难度较高的游戏中，玩家可能不能利用以上简单的推论方法来解谜。这时玩家可以先假定一个空格为需要填上的，然后继续解答。但当遇到矛盾的话，玩家需要把游戏回退到假定前的状态，因为矛盾证明了之前的假定是错误的。玩家亦可把该空格标空，因为它一定不是需要填充的格了。

多重答案

有些数织可以有多个可行的答案（踩地雷也会有这种情况）。不过并不是所有答案都是有意思的图像。

一个简单的例子就是以数织记录的国际象棋棋盘。为了方便阅读和编辑，以下的棋盘大小只是平常的四分之一。

答案一：

1
1 		1
1 		1
1 		1
1
1 1 × ×
1 1 × ×
1 1 × ×
1 1 × ×

答案二：

1
1 		1
1 		1
1 		1
1
1 1 × ×
1 1 × ×
1 1 × ×
1 1 × ×

变种

也有一种彩色版的逻辑拼图游戏，谜题中有多种颜色的色块，并从而取消了传统黑白版（英语：R&B）中的空白格设计。

外部链接