赵友钦割圆术是元代数学家赵友钦在所著的《革象新书》卷五《乾象周髀》篇研究的割圆术。与刘徽从内接正六角形开始不同,赵氏割圆术从分割内接正方形开始[1]。
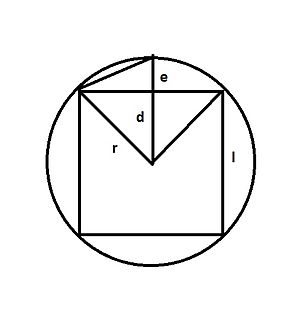
如图,圆的半径为r; 内接正方形的边长为  ,由圆心到正方形一边倒垂直距离为 d
,由圆心到正方形一边倒垂直距离为 d


d 的延长线与圆周相交点将圆周等分为正八边形。
令正八边形的边长为


设 为分割圆成正16边形之边长,赵友钦正确地推断
为分割圆成正16边形之边长,赵友钦正确地推断 与
与 的迭代关系:
的迭代关系:

推而广之:

令 r=1;





……
南朝祖冲之发现密率:
但这个密率比在以后数百年间,无人问津,直到赵友钦重新提及这个密率分数[2]。
赵友钦在获得
后,他将 3141.592 乘以 113
以一百一十三乘之果得三百五十五尺,此为其法所以极精密也
即: