欧拉线

如图${\displaystyle H,G,O}$ 分别是${\displaystyle {\triangle }ABC}$ 的垂心，重心，外心。

设${\displaystyle D}$ 为直线${\displaystyle BO}$ 和${\displaystyle {\triangle }ABC}$ 外接圆的交点，并连结${\displaystyle AH,AD,CD,CH}$ 。

（1） ${\displaystyle {\because \quad }BD}$ 是直径，${\displaystyle {\therefore \quad }CD{\perp }BC}$ 且${\displaystyle AD{\perp }AB}$ 。

又${\displaystyle H}$ 是垂心，${\displaystyle {\therefore \quad }AH{\perp }BC}$ 且${\displaystyle CH{\perp }AB}$ 。

${\displaystyle {\therefore \quad }CD//AH}$ ，${\displaystyle AD//CH}$ 。

${\displaystyle ADCH}$ 为平行四边形。

->${\displaystyle AH=DC}$ 

又${\displaystyle O,\;M}$ 分别是${\displaystyle BD,\;CB}$ 的中点，

${\displaystyle {\therefore \quad }DC=2OM}$ ， ${\displaystyle AH=2OM}$ 

（2） 作${\displaystyle BC}$ 边上的中线${\displaystyle AM,}$ 连结${\displaystyle OM,\;OH}$ 

设${\displaystyle OH}$ 交${\displaystyle AM}$ 于点${\displaystyle G'}$ 

${\displaystyle {\because \quad }OM{\perp }BC,\;{\triangle }AHG'{\sim \triangle }MOG',\;AH=DC=2OM}$ ，

${\displaystyle {\therefore \quad }AG'=2G'M}$ ，

${\displaystyle {\therefore \quad }G'}$ 即${\displaystyle \triangle ABC}$ 的重心${\displaystyle G}$ 

${\displaystyle \therefore \quad \triangle ABC}$ 的垂心${\displaystyle H,}$ 重心${\displaystyle G,}$ 外心${\displaystyle O}$ 三点共线${\displaystyle ,}$ 直线${\displaystyle HGO}$ 即欧拉线

九点圆的圆心也在欧拉线上，且在垂心到外心的线段的中点

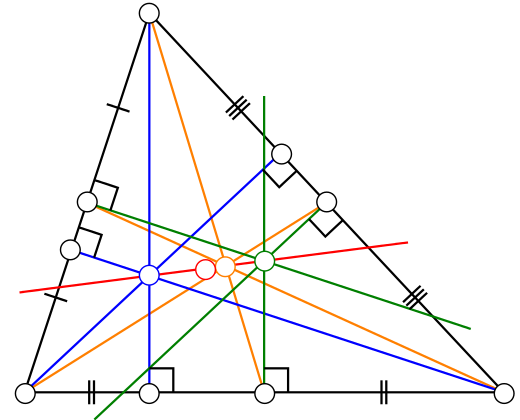
如图，H、G、Ω分别是△ABC的垂心、重心、外心，三角形的三边中点I _i，三高的垂足H_i，和顶点到垂心的三条线段的中点J _i

令HΩ和J₁I₁的交点为K，∵BΩ=CΩ，BI₁=CI₁，∴ΩI₁⊥BC，又∵AH₁⊥BC，∴ΩI₁∥AH₁。

∵∠GΩI₁=∠AHG，∠GAH=∠GI₁Ω，∴△AGH∽△GΩI₁。∵AG=2GI₁，∴AH=2ΩI₁，即ΩI₁=J₁H。

∵ΩI₁∥AH₁， J₁H=ΩI₁ ∴J₁K=KI₁, HK = KΩ。

同理J₂K=KI₂， J₃K=KI₃。 可知K为九点圆圆心。

∵点K在HΩ上，HK = KΩ

∴九点圆圆心在欧拉线上，且在垂心到外心的线段的中点。

1. 数学题解辞典·平面几何. 上海辞书出版社. 

• Altitudes and the Euler Line （页面存档备份，存于互联网档案馆）
• Euler Line and 9-Point Circle （页面存档备份，存于互联网档案馆）