卡诺定理

设ABC为三角形，O为其外心。则O到ABC各边的距离之和为

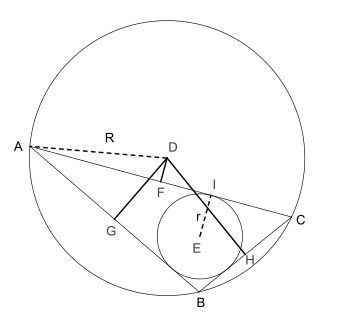
{\begin{aligned}&{}\qquad DG+DH+DF\\&{}=|DG|+|DH|-|DF|\\&{}=R+r\end{aligned}}

OO_A + OO_B + OO_C = R + r，

其中r为内切圆半径，R为外接圆半径。这个定理叫做卡诺定理（法语：Théorème de Carnot），以拉扎尔·卡诺为名。

引理

在 $\triangle ABC$ 中， $R$ 为 $\triangle ABC$ 之外接圆半径，且 $r$ 为 $\triangle ABC$ 之内切圆半径，则

r=4R\sin({\frac {A}{2}})\sin({\frac {B}{2}})\sin({\frac {C}{2}})

证明

假设 $\triangle ABC$ 为锐角三角形， $D$ 为 $\triangle ABC$ 之外接圆圆心， $D$ 至 $\triangle ABC$ 三边之距离分别为 ${\overline {DG}}$ 、 ${\overline {DH}}$ 、 ${\overline {DF}}$ ，其中 ${\overline {DG}}$ 为 $D$ 至 ${\overline {AB}}$ 之距离， ${\overline {DH}}$ 为 $D$ 至 ${\overline {BC}}$ 之距离， ${\overline {DF}}$ 为 $D$ 至 ${\overline {AC}}$ 之距离。连接 $D$ 与 $B$ ，在 $\triangle HDB$ 中，根据三角形外心性质，可以得到

{\overline {DB}}=R

\angle {HDB}=\angle {A}

所以，可以得到 ${\overline {DH}}$ 的表示式，

{\overline {DH}}=R\cos(A)

同理，亦可得到 ${\overline {DG}}$ 和 ${\overline {DF}}$ 的表示式，

{\overline {DG}}=R\cos(C)

{\overline {DF}}=R\cos(B)

因此，

{\overline {DG}}+{\overline {DH}}+{\overline {DF}}\,

=R(\cos(A)+\cos(B)+\cos(C))\,

=R(2\cos({\frac {A+B}{2}})\cos({\frac {A-B}{2}})+1-2\sin ^{2}({\frac {C}{2}}))\,

=R(2\cos({\frac {\pi -C}{2}})\cos({\frac {A-B}{2}})+1-2\sin({\frac {\pi -(A+B)}{2}})\sin({\frac {C}{2}}))\,

=R(2\sin({\frac {C}{2}})\cos({\frac {A-B}{2}})+1-2\cos({\frac {(A+B)}{2}})\sin({\frac {C}{2}}))\,

=R(2\sin({\frac {C}{2}})(\cos({\frac {A-B}{2}})-\cos({\frac {(A+B)}{2}}))+1)\,

=R(4\sin({\frac {A}{2}})\sin({\frac {B}{2}})\sin({\frac {C}{2}})+1)\,

=4R\sin({\frac {A}{2}})\sin({\frac {B}{2}})\sin({\frac {C}{2}})+R\,

根据引理，即可得证，

{\overline {DG}}+{\overline {DH}}+{\overline {DF}}=R+r

此外，若 $\triangle ABC$ 为钝角三角形，且 $\angle {B}$ 大于 $90$ 度，其余符号假设均与上面相同，则可以得到，

{\overline {DH}}=R\cos(A)\,

{\overline {DF}}=R\cos(\pi -B)=-R\cos(B)\,

{\overline {DG}}=R\cos(C)\,

所以，

{\overline {DG}}+{\overline {DH}}-{\overline {DF}}\,

=R(\cos(A)+\cos(B)+\cos(C))\,

=R+r\,

故得证卡诺定理。