蚌线
蚌线(英语:conchoid)是由一个不动点O、另外一条曲线,以及一个长度d导出的曲线,另一条曲线,长度为d。它是由古希腊数学家尼科米迪斯发明的。[1]
轨迹定义
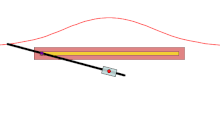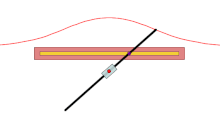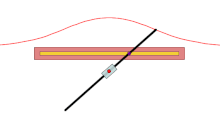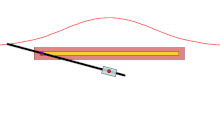
过定点O的直线交不过O的定直线l(l与O的距离为a)于Q,在OQ上取P,使|QP|=b(b是常数),则P的轨迹称为蚌线。
特征
- 蚌线有内外两支。
- a和b的大小关系,蚌线有三种不同形态。
曲线方程
极坐标方程
ρ = a ± b secθ
- O为极点;
- O到l的离差的方向为极轴
- a、b为实数
- -π / 2 ≤ θ ≤ π / 2时,
- ρ = a + b secθ表示曲线的外支;
- ρ = a –b secθ表示曲线的内支。
直角坐标方程
- O为原点;
- 直线l方程为x = a;
利用蚌线可以三等分角。
参见
- 一般蚌线