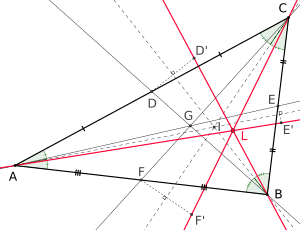
类似中线

在一个三角形中，类似中线是一组（共三条）特殊直线。他们分别是三条中线（顶点和对边中点的连线）关于顶点角平分线的反射。这三条类似中线交于三角形内部一点，称为三角形的类似重心或莱莫恩点，后者以法国数学家埃利·莱莫恩（英语：Émile Lemoine）命名，他证明了这个点的存在性。

一个三角形的中线（蓝色）角平分线（绿色）和类似中线（红色），类似中线交于类似重心 L。

特殊点

一个边长为 a、b 和 c 三角形的类似重心有齐次三线坐标 [a : b : c]。

三角形的Gergonne点和三角形的内接三角形的类似重心重合。

类似重心是三角形的重心的等角共轭点。

参考

  • Ross Honsberger, "The Symmedian Point," Chapter 7 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry, The Mathematical Association of America, Washington, D.C., 1995.

外部链接