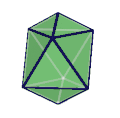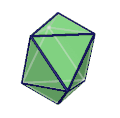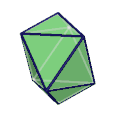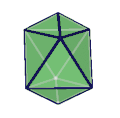
截对角三方偏方面体

在 几何学中， 截对角三方偏方面体是截对角偏方面体这一系列的多面体中的第一个。它有六个五边形，两个三角形。

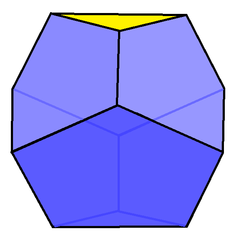截对角三方偏方面体
截对角三方偏方面体
又称杜勒多面体
类别截对角偏方面体
对偶多面体双三角锥反角柱
性质
面8
边18
顶点12
欧拉特征数F=8, E=18, V=12 （χ=2）
组成与布局
面的种类6个五边形
2个三角形
特性
凸
图像
双三角锥反角柱.gif
双三角锥反角柱
（对偶多面体）

几何学中

此多面体可透过将一个立方体，或是三方偏方面体，或是一个菱面体，或一个平行六面体中一对处于对角位置的顶点切除，在立方体或著三方偏方面体的例子中，由于截面是平行的，以及原像的高度对称，因此具有高度的旋转对称。

杜勒多面体

 
《忧郁 I》

这个多面体有时候也称为杜勒立体或杜勒多面体（Dürer's solid），因为它出现于阿尔布雷希特·杜勒的 1514年画像《忧郁 I》。这图像亦称杜勒图（英语：Dürer graph）。

关于杜勒所描述的立体形状是一些学术辩论的主题。[注 1] 依照Lynch (1982)，他假设该立体是一个立方体的截角的误绘，该点子源于Strauss (1972)； 然而大部分的来源资料同意其为菱面体的截角。 尽管有着这样的同意，而这个菱面体在几何学中确切的形状是许多矛盾的理论的主题。

  • Richter (1957)声称杜勒多面体的原像菱面体中的菱形面的两条对角线的比是 5:6，而这个数值所产生出来的菱形，其锐角的角度大约为80°[1]。
  • Schröder (1980)以及Lynch (1982)在1980年代时认为该菱形对角线长的比应该是 而此数值产生出来的菱形，其锐角的角度会变成大约 82°[2][3]。
  • MacGillavry (1981)时，测量了该图形的特征并测量出该菱形的锐角大约为 79°。他以及一位后来的另一位作者，沃尔夫·冯·恩格尔哈特（英语：Wolf von Engelhardt） （参见 Hideko (2009)）认为该角度的形成取决于自然形成的方解石结晶[4]。
  • Schreiber (1999)认为根据杜勒的著作，所有的顶点应该是坐落在同一个球面上， 并更进一步的声明该菱形的锐角为 72°[5]。 Hideko (2009)列举了其他几位同样赞同该菱形锐角为72°的学者，从1955年的保罗·格罗津斯基（Paul Grodzinski）开始。他认为，这种理论的动机少于实际绘图的分析，而比较倾向关于五边形以及黄金比例的审美原则[3]。
  • Weitzel (2004) 分析了对于同一个立体的1510年的草图， 从中他确认了薛伯的假设，即该立体有一个 外接球 但菱形的锐角角度会是大约79.5°[2]。
  • Hideko (2009)认为该形状是为了描述一个著名的几何学问题，倍立方体的解答，而杜勒也在1525年中提到。 他随后总结出（在两个顶点截去前）该立体是一个立方体沿着对角线伸长而成的。 更具体地说，他认为杜勒绘制了一个实际的立方体，长对角线平行于图形平面（英语：Picture plane），然后在长对角线的方向上以因为某种因素而放大他的绘画：结果会和他绘制一个被延长的图形相同。放大的因素是因为关于倍立方后的体积是原立方体的 21/3 ≈ 1.253，但秀子导出不同的，为了适应图纸的放大因素，1.277，以一个更复杂的方式[3]。
  • Futamura，Frantz & Crannell (2014)将所提出的解决方案分类为该问题，透过两个参数：锐角以及切面，称为交比。 他们估算这个交比很接近麦克·盖勒艾瑞的，而且具有一个接近 黄金比例的数值。 基于这一点，他们认为锐角是  而交比是精确的  [6]。

参见

  • 倒角四面体：另一个将立方体的顶点交错截角的多面体。

注译

  1. ^ 参见 Weitzel (2004) 以及 Ziegler (2014)，从中得出以下许多历史事件。

参考资料

  1. ^ Richter, D. H., Perspektive und Proportionen in Albrecht Dürers "Melancholie", Z. Vermessungswesen, 1957, 82: 284–288 and 350–357 . As cited by Weitzel (2004)
  2. ^ 2.0 2.1 Schröder, E., Dürer, Kunst und Geometrie, Dürers künstlerisches Schaffen aus der Sicht seiner "Underweysung", Basel, 1980 . As cited by Weitzel (2004).
  3. ^ 3.0 3.1 3.2 Lynch, Terence, The geometric body in Dürer's engraving Melencolia I, Journal of the Warburg and Courtauld Institutes (The Warburg Institute), 1982, 45: 226–232, JSTOR 750979, doi:10.2307/750979 
  4. ^ MacGillavry, C., The polyhedron in A. Dürers Melencolia I, Nederl. Akad. Wetensch. Proc. Ser. B, 1981, 84: 287–294 . As cited by Weitzel (2004)
  5. ^ Schreiber, Peter, A new hypothesis on Dürer's enigmatic polyhedron in his copper engraving "Melencolia I", Historia Mathematica, 1999, 26: 369–377, doi:10.1006/hmat.1999.2245 .
  6. ^ Futamura, F.; Frantz, M.; Crannell, A., The cross ratio as a shape parameter for Dürer's solid, Journal of Mathematics and the Arts, 2014, 8 (3-4): 111–119, arXiv:1405.6481  , doi:10.1080/17513472.2014.974483 .
  1. Strauss, Walter L., The Complete Engravings of Dürer, New York: 168, 1972, ISBN 0-486-22851-7 . As cited by Lynch (1982).
  2. Weber, P., Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus, Strassburg, 1900 . As cited by Weitzel (2004).
  3. Weitzel, Hans, A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I, Historia Mathematica, 2004, 31 (1): 11–14, doi:10.1016/S0315-0860(03)00029-6 .
  4. Hideko, Ishizu, Another solution to the polyhedron in Dürer's Melencolia: A visual demonstration of the Delian problem (PDF), Aesthetics (The Japanese Society for Aesthetics), 2009, 13: 179–194 [2017-02-23], （原始内容存档 (PDF)于2018-02-19） .
  5. Ziegler, Günter M., Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube, Alex Bellos's Adventures in Numberland, The Guardian, December 3, 2014 [2017-02-23], （原始内容存档于2020-11-11） .

外部链接