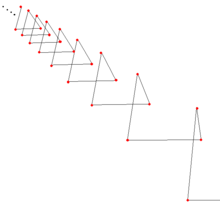
扭歪无限边形
在几何学中,扭歪[1]无限边形(英语:Skew apeirogon)又称歪斜无限边形、挠无限边形[2]是一种顶点并非全部共线的无限边形。
较常讨论及研究的扭歪无限边形主要有两个不同维度的形式,一种是二维的锯齿歪斜无限边形(英语:zig-zag skew apeirogons)其顶点交错位于两条互相平行的直线上,另一种是三维的螺旋歪斜无限边形(英语:helical skew apeirogons)其顶点位于一个圆柱面上。二维中的锯齿歪斜无限边形可以看做是不断平移镜射[3],如三维空间的螺旋轴对称的形状。
二维的正扭歪无限边形
| 正扭歪无限边形 | |
|---|---|
| 类型 | 正扭歪多边形 |
| 对偶 | 正无限边形 |
| 边 | ∞ |
| 顶点 | ∞ |
| 施莱夫利符号 | {∞}#{ } |
| 对称群 | D∞d, [2+,∞], (2*∞) |
| 内角(度) | 扭歪 |
| 特性 | 扭歪, 等边多边形, 等角多边形 |
位于二维空间的正扭歪无限边形是一种锯齿扭歪多边形,又称为正锯齿扭歪无限边形具有2*∞, D∞d带状群的对称性。
正的扭歪无限边形存在于三种正镶嵌图的皮特里多边形中,包括正方形镶嵌、正三角形镶嵌以及正六边形镶嵌,其内角分别为90°、120°和60°分别来自各正镶嵌图里的正多边形。
等角扭歪无限边形
等角扭歪无限边形具有两种不同的边交错出现在带状群的对称性中,可以看成将正锯齿扭歪无限边形扭曲成具有平移对称性的等角无限边形。
| 对称性: p1, [∞]+, (∞∞), C∞ | |
|---|---|
| |
|
另外还有一种等角扭歪无限边形,其两种不同的边其中一种边交错的与两条相互平行的直线重和(共线),每个平行边的中垂线都是整个图形的镜射轴。若边都等长则可以称其为半正扭歪无限边形。
| 对称性: p2mg, [2+,∞], (2*∞), D∞d | ||
|---|---|---|
| |
|
|
半正扭歪无限边形存在于一些平面正镶嵌图或半正镶嵌图的皮特里多边形中:
双曲面上的扭歪无限边形
如同平面几何,在双曲几何中也能找到扭歪无限边形。
在双曲面上的正扭歪无限边形与平面的正扭歪无限边形类似,一样是存在于双曲面上正镶嵌图的皮特里多边形中,双曲面半正扭歪无限边形也一样,存在于双曲面上半正镶嵌图的皮特里多边形中。
三维空间的扭歪无限边形
| 正螺旋无限边形 | |
|---|---|
| 三角螺旋无限边形 | |
| 类型 | 正扭歪多边形 |
| 对偶 | 螺旋无限边形 (本身) |
| 边 | ∞ |
| 顶点 | ∞ |
| 施莱夫利符号 | {∞}#{p} |
| 对称群 | 螺旋轴对称 |
| 内角(度) | 扭歪 |
| 特性 | 扭歪, 等边多边形, 等角多边形 |
三维空间的扭歪无限边形是一种顶点全部局限于一个圆柱面的螺旋状几何图形,称为螺旋无限边形
这种扭歪无限边形可以借由无限堆叠的半正柱体或反柱体来构造,一般其扭曲角并不限于180度的整数除数。这种扭歪无限边形具有螺旋轴对称的对称性。
无限堆叠的柱体,比如无限堆叠的正方体,透过每个正方形面的对角线相连,环绕着无限堆叠的正方体而构成一个四角螺旋无限边形,其扭曲角为90度,在施莱夫利符号中以{∞}#{4}表示
无限堆叠的反柱体,比如无限堆叠的正八面体,透过每个边螺旋地环绕着无限堆叠的正八面体相连,而构成,根据连的边不同,一共有三种不同的组合,分别以红色、绿色和蓝色三种颜色表示。其扭曲角为60度,在施莱夫利符号中以{∞}#{6}表示
等角螺旋无限边形
参考文献
- McMullen, Peter; Schulte, Egon, Abstract Regular Polytopes 1st, Cambridge University Press, December 2002, ISBN 0-521-81496-0 p. 25
- Coxeter, H.S.M.; Regular complex polytopes (1974). Chapter 1. Regular polygons, 1.5. Regular polygons in n dimensions, 1.7. Zigzag and antiprismatic polygons, 1.8. Helical polygons. 4.3. Flags and Orthoschemes, 11.3. Petrie polygons
- Coxeter, H. S. M. Petrie Polygons. Regular Polytopes, 3rd ed. New York: Dover, 1973. (sec 2.6 Petrie Polygons pp. 24–25, and Chapter 12, pp. 213–235, The generalized Petrie polygon )
- Coxeter, H. S. M. & Moser, W. O. J. Generators and Relations for Discrete Groups. New York: Springer-Verlag. 1980. ISBN 0-387-09212-9. (1st ed, 1957) 5.2 The Petrie polygon {p,q}.
- ^ 400年ぶりに新種の「対称性多面体」構造が発見される. gigazine.net. 2014-02-22 [2016-07-16]. (原始内容存档于2020-11-19).
- ^ skew polygon meaning in Chinese. ichacha.net. [2016-07-16]. (原始内容存档于2019-06-03).
- ^ Coxeter, H. S. M. and Moser, W. O. J. (1980), p.54 5.2 The Petrie polygon
- ^ Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, 互联网档案馆) (Definition: paper 13, Discrete groups generated by reflections, 1933, p. 161)