假如我们想得到未知函数 f 在点 的值,假设我们已知函数 f 在 , , , 及 四个点的值。
首先在 x 方向进行线性插值,得到
-
然后在 y 方向进行线性插值,得到
-
注意此处如果先在 y 方向插值、再在 x 方向插值,其结果与按照上述顺序双线性插值的结果是一样的。
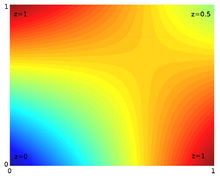
单位正方形
如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
-
或者用矩阵运算表示为
-
非线性
顾名思义,双线性插值的结果不是线性的,它是两个线性函数的积。在单位正方形上,双线性插值可以记作
-
常数的数目(四)对应于给定的 f 的数据点数目
-
-
-
-
双线性插值的结果与插值的顺序无关。首先进行 y 方向的插值,然后进行 x 方向的插值,所得到的结果是一样的。
双线性插值的一个显然的三维空间延伸是三线性插值。