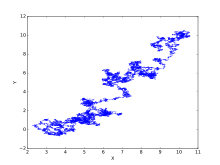
奥恩斯坦-乌伦贝克过程

在数学中，奥恩斯坦-乌伦贝克过程（Ornstein-Uhlenbeck process，简称OU过程）是一个随机过程，在金融数学和物理学中有很多的引用。OU过程描述一个经历摩擦的布朗粒子（damped random walk）。^[1]

这个过程以奥恩斯坦（Leonard Ornstein）和乔治·乌伦贝克的名字命名。

这是一个自回归模型AR(1)。

θ =1.0，σ =3和μ =(0,0) 粒子在(10,10)开始

定义

θ =1.0，σ =3, μ =(0,0,0) 粒子在(10,10,10)开始

OU过程有下面的随机微分方程

$dx_{t}=-\theta \,x_{t}\,dt+\sigma \,dW_{t}$

其中的 $\theta >0$ ， $\sigma >0$ 是参数，并且 $W_{t}$ 是维纳过程。^[2]^[3]^[4]

$dx_{t}=\theta (\mu -x_{t})\,dt+\sigma \,dW_{t}$

$\mu$ 是常值。上面的方程是Vasicek模型。^[5]

福克–普朗克方程

OU过程的福克–普朗克方程是^[6]

${\frac {\partial P}{\partial t}}=\theta {\frac {\partial }{\partial x}}(xP)+D{\frac {\partial ^{2}P}{\partial x^{2}}}$

$D=\sigma ^{2}/2$ 。这是一个抛物偏微分方程。方程的解是

$P(x,t\mid x',t')={\sqrt {\frac {\theta }{2\pi D(1-e^{-2\theta (t-t')})}}}\exp \left[-{\frac {\theta }{2D}}{\frac {(x-x'e^{-\theta (t-t')})^{2}}{1-e^{-2\theta (t-t')}}}\right]$

三个OU进程，θ = 1, μ = 1.2, σ = 0.3:
蓝：在a = 0 开始（几乎必然）
绿：在a=2开始
红：初始值呈正态分布

参考文献

^ MacLeod, C. L.; Ivezić, Ž; Kochanek, C. S.; Kozłowski, S.; Kelly, B.; Bullock, E.; Kimball, A.; Sesar, B.; Westman, D. Modeling the Time Variability of SDSS Stripe 82 Quasars as a Damped Random Walk. The Astrophysical Journal. October 2010, 721: 1014. doi:10.1088/0004-637X/721/2/1014 （英语）. ^{[永久失效链接]}
^ Karatzas, Ioannis; Shreve, Steven E., Brownian Motion and Stochastic Calculus 2nd, Springer-Verlag: 358, 1991, ISBN 978-0-387-97655-6
^ Gard, Thomas C., Introduction to Stochastic Differential Equations, Marcel Dekker: 115, 1988, ISBN 978-0-8247-7776-0
^ Gardiner, C.W., Handbook of Stochastic Methods 2nd, Springer-Verlag: 106, 1985, ISBN 978-0-387-15607-1
^ Björk, Tomas. Arbitrage Theory in Continuous Time 3rd. Oxford University Press. 2009: 375, 381. ISBN 978-0-19-957474-2.
^ Risken, H., The Fokker-Planck Equation: Methods of Solution and Application, Springer-Verlag: 99–100, 1984, ISBN 978-0-387-13098-9
^ Chan et al. (1992)

阅读

Bibbona, E.; Panfilo, G.; Tavella, P. The Ornstein-Uhlenbeck process as a model of a low pass filtered white noise. Metrologia. 2008, 45 (6): S117–S126. Bibcode:2008Metro..45S.117B. doi:10.1088/0026-1394/45/6/S17.
Chan, K. C.; Karolyi, G. A.; Longstaff, F. A.; Sanders, A. B. An empirical comparison of alternative models of the short-term interest rate. Journal of Finance. 1992, 47 (3): 1209–1227. doi:10.1111/j.1540-6261.1992.tb04011.x.
Doob, J.L. The Brownian Movement and Stochastic Equations. Annals of Mathematics. April 1942, 43 (2): 351–369. JSTOR 1968873. doi:10.2307/1968873.
Gillespie, D. T. Exact numerical simulation of the Ornstein–Uhlenbeck process and its integral (PDF). Phys. Rev. E. 1996, 54 (2): 2084–2091 [2020-02-11]. Bibcode:1996PhRvE..54.2084G. PMID 9965289. doi:10.1103/PhysRevE.54.2084. （原始内容 (PDF)存档于2022-03-01）.
Leung, Tim; Li, Xin. Optimal Mean Reversion Trading with Transaction Costs and Stop-Loss Exit. International Journal of Theoretical & Applied Finance. 2015, 18 (3): 1550020. arXiv:1411.5062  . doi:10.1142/S021902491550020X.
Risken, H. The Fokker–Planck Equation: Method of Solution and Applications. New York: Springer-Verlag. 1989. ISBN 978-0387504988.
Uhlenbeck, G. E.; Ornstein, L. S. On the theory of Brownian Motion. Phys. Rev. 1930, 36 (5): 823–841. Bibcode:1930PhRv...36..823U. doi:10.1103/PhysRev.36.823.
Martins, E.P. Estimating the Rate of Phenotypic Evolution from Comparative Data. Amer. Nat. 1994, 144 (2): 193–209.

外部链接

Review of Statistical Arbitrage, Cointegration, and Multivariate Ornstein–Uhlenbeck （页面存档备份，存于互联网档案馆）, Attilio Meucci
A Stochastic Processes Toolkit for Risk Management, Damiano Brigo, Antonio Dalessandro, Matthias Neugebauer and Fares Triki
Simulating and Calibrating the Ornstein–Uhlenbeck process, M. A. van den Berg
Maximum likelihood estimation of mean reverting processes （页面存档备份，存于互联网档案馆）, Jose Carlos Garcia Franco
Interactive Web Application: Stochastic Processes used in Quantitative Finance. [2015-07-03]. （原始内容存档于2015-09-20）.

[1] MacLeod, C. L.; Ivezić, Ž; Kochanek, C. S.; Kozłowski, S.; Kelly, B.; Bullock, E.; Kimball, A.; Sesar, B.; Westman, D. Modeling the Time Variability of SDSS Stripe 82 Quasars as a Damped Random Walk. The Astrophysical Journal. October 2010, 721: 1014. doi:10.1088/0004-637X/721/2/1014 （英语）. ^{[永久失效链接]}

[2] Karatzas, Ioannis; Shreve, Steven E., Brownian Motion and Stochastic Calculus 2nd, Springer-Verlag: 358, 1991, ISBN 978-0-387-97655-6

[3] Gard, Thomas C., Introduction to Stochastic Differential Equations, Marcel Dekker: 115, 1988, ISBN 978-0-8247-7776-0

[4] Gardiner, C.W., Handbook of Stochastic Methods 2nd, Springer-Verlag: 106, 1985, ISBN 978-0-387-15607-1

[5] Björk, Tomas. Arbitrage Theory in Continuous Time 3rd. Oxford University Press. 2009: 375, 381. ISBN 978-0-19-957474-2.

[6] Risken, H., The Fokker-Planck Equation: Methods of Solution and Application, Springer-Verlag: 99–100, 1984, ISBN 978-0-387-13098-9

[7] Chan et al. (1992)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

奥恩斯坦-乌伦贝克过程

目录

定义

福克–普朗克方程

相关

参考文献

阅读

外部链接