马赫－曾德尔干涉仪

马曾干涉仪的内部设置可以很容易更改。与迈克耳孙干涉仪明显不同，两道被分裂的光束只会分别行经一次马曾干涉仪的两条严格分隔的路径。

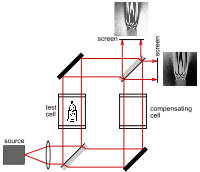
由于白光的相干长度很有限，数量级为微米，必须非常仔细的将白光的所有波长的光程都调整为一样，才能通过马曾干涉仪将白光制成黑白相间的干涉条纹，否则无法观察到干涉条纹。如首段火焰图所示，一个同样玻璃材质的“补偿盒”被置入参考光束的路径来匹配“检验盒”，这样，两个盒子的光学色散可以调整为一样。注意到两个分束器的精确取向，两个分束器的反射表面应该有完全相反取向（一个面向左上方，一个面向右下方），这样，检验光束与参考光束会透射过同样厚度的玻璃。由于检验光束与参考光束都经历到两个“空气－镜面的界面反射”，造成同样的相移，因此，在最右方屏幕会形成相长干涉图样，显示为白色火焰；而在最上方屏幕会另外形成相消干涉图样，显示为黑色火焰。^[3][4]

准直光源会形成非局域条纹图案；延伸光源会形成局域条纹图案。仔细调整镜子与分束器的取向，即可使干涉条纹形成于指定局域位置。^[6]:18对于大多数案例，通过调整的动作，可使干涉条纹形成的平面与检验物体同面，这样，两者可以一起成像。

马曾干涉仪的内部工作空间相当宽广，干涉条纹的形成位置有很多种选择，因此，它是观察在风洞里气体流动的佳选。^[7][8]对于一般流动可视化研究，也是很好选择。它时常被用于空气动力学、等离子物理学与传热学领域，可以测量气体的压强、密度和温度的变化。^{[6]:18,93–95}

马曾干涉仪时常被用来研究量子纠缠──量子力学的最反直觉的预测之一。^[9][10]

仪器内构

一道准直光束被第一块半镀银镜分裂成两道光束，称为“样品光束”与“参考光束”。这两道光束分别被两块镜子反射后，又通过同样的第二块半镀银镜，然后进入检测器。

除了最后一块半镀银镜以外，所有全镀银镜与半镀银镜的表面都是面对入射光束。最后一块半镀银镜的表面是面对透射过第一块半镀银镜的光束。

性质

菲涅耳方程描述关于波动在界面的反射行为与透射行为。菲涅耳方程表明，假若传播于低折射率介质的波动遇到了高折射率介质，则波动的相位会被改变；假若传播于高折射率介质的波动遇到了低折射率介质，则波动的相位不会被改变。换句话说，

• 假若波动从空气传播遇到镜子表面的镀膜，则反射波的相移为 ${\displaystyle \pi }$  角弧，因为镀膜的折射率高于空气的折射率。
• 假若波动从从镜子后部的玻璃传播遇到镜子表面的镀膜，则反射波的相移为零，因为镀膜的折射率低于玻璃的折射率。

除了这重要相移机制以外，对于光波而言，

• 在折射率大于真空折射率（数值为1）的介质内，光波传播的速度较慢，它的速度 ${\displaystyle v}$  为 ${\displaystyle v=c/n}$  ；其中， ${\displaystyle c}$  是光速， ${\displaystyle n}$  是介质的折射率。这会造成相移，其大小与 ${\displaystyle (n-1)d}$  成正比；其中， ${\displaystyle d}$  是光波传播于介质内部的距离。
• 假若通过镜子后部的玻璃会造成常数相移 ${\displaystyle k}$  ，则从镜子后部的玻璃遇到镜子表面的镀膜反射回来所遭到的相移为 ${\displaystyle 2k}$  ，这是因为光波传播于镜子后部的玻璃，然后遇到镜子表面的镀膜，这会造成相移 ${\displaystyle k}$  ，而反射的动作不会造成任何位移，之后，光波从镜子表面的镀膜传播于镜子后部的玻璃又会造成相移 ${\displaystyle k}$  。

另外，还有一些必需注意的细节。上述关于相移的规则适用于采用介电质镀膜的分束器，假若采用的是金属镀膜，或者不同的偏振必需被纳入考量，则该规则必须加以修改。对于真实干涉仪，分束器的厚度不同，因此两条路径的长度可能不一样。不论如何，假若光波不会被吸收，则能量守恒定律保证，抵达检测器1的光波所遭到的相移差 ${\displaystyle \Delta \phi _{1}}$  与抵达检测器2的光波所遭到的相移差 ${\displaystyle \Delta \phi _{2}}$  ，两个相移差遵守关系式^[3]

${\displaystyle |\Delta \phi _{1}-\Delta \phi _{2}|=\pi }$ 。

样品的效应

在马曾干涉仪实验范例图里，假设样品尚未置入，则样品光束SB与参考光束RB会抵达检测器1同相，因此形成相长干涉。两个光束的相移为 ${\displaystyle 2\pi +k}$  ，因为从空气遇到镜子表面而产生的反射有两次，穿透过玻璃有一次。

假设样品尚未置入，样品光束SB与参考光束RB会抵达检测器2异相，因此形成相消干涉，不会检测道光束。抵达检测器2的样品光束SB会遭到相移 ${\displaystyle 2\pi +2k}$  ，因为从空气遇到镜子表面而产生的反射有两次，从镜子后部遇到镜子表面而产生反射有一次。抵达检测器2的参考光束RB会遭到相移 ${\displaystyle \pi +2k}$  ，因为从空气遇到镜子表面而产生的反射有一次，穿透过玻璃有两次。

现在将样品置入样品光束路径，则两个检测器会感受到不同的辐照度，从这不同可以计算出样品造成的相移。

由于马赫－曾德尔干涉仪具有多功能性质，它被广泛应用在量子力学的基础研究论题里，例如，对于反事实确定性、量子纠缠、伊利泽-威德曼炸弹测试问题、量子擦除实验、量子芝诺效应、中子衍射的研究。

• 法布里－珀罗干涉仪
• 迈克耳孙干涉仪
• 迈克耳孙测星干涉仪